Yo no sé casi nada de computación cuántica.
Lo que comentaré aquí es una opinión personal y poco relevante por ni nivel de desconocimiento
No me hago responsable de las consecuencias que pueda tener que alguien me haga caso
Dicho esto...
El bogosort del comentario anterior, para mi es un buen ejemplo de lo que es computación cuántica.
Esto es un tema muy de moda.
Hay mucha gente investigando y ganando premios (y mucho dinero)
Probablemente porque de ser posible la computación cuántica... la gente tiene miedo de quedarse rezagados en algo tan rompedor
BASES DE LA COMPUTACIÓN CUÁNTICA...
* Tenemos unos cuantos qbits
* Están "relacionados" entre sí de forma que sólo pueden coexistir con valores concretos cuando se cumple la solución del problema a resolver (ejemplo habitual, la factoriazación)
Un qbit es un bit cuántico, que puede tener (y habitualmente tiene) los dos valores posibles al mismo tiempo
Por tanto, un grupo de 32 qbits, representan en todo momento todos los números posibles con 32 bits
Eso es fantástico y mucho mejor que el sistema "antiguo", donde con 32 bits, sólo puedes representar un caso concreto
Pero hasta el momento esto es poco práctico.
Si sumamos un número de 32qbits a otro de 32qbits y el resultado lo tenemos en 33qbits...
Pues no se moleste oiga, coje 33qbits y ya tienes todas las posibles sumas de números de 32bits
Y después de esta chorrada metafísica que no sirve para nada...
¿Como narices se puede hacer que los qbits sean prácticos?
Pongamos un ejemplo complicado
Tenemos 3 grupos de 32qbits
El grupo 1 y el 2 están "relacionados" con el 3 de forma que sólo admite valores en los que g1 y g2 son factores de 3
Ahora le damos un valor a g3 y voalá...
g1 y g2 tiene inmediatamente dos factores del número representado en g3
Fantástico, pero hay un par de problemas...
PROBLEMA 1
==============
¿Cómo los "relacionamos" para este fin?
Complicado, pero se sabe que en determinados casos pueden haber propiedas cuánticas "relacionadas"
Supongamos que se puede hacer
PROBLEMA 2
==============
¿Me tengo que creer que asignado unos valores en unos qbits otros dejan de tener valores simultáneos?
Ahí está el gatito de Schrodinger y la famosa interpretación de Acapulco (me gusta pensar que estaban en la playa mientras definían estas cosas complicadas)
Más o menos dicen.
El gato está vivo y muerto a la vez mientras nadie lo observe.
Una vez que lo miramos, el gato estará vivo o muerto
Pero eso no es ciencia.
No se puede verificar, no sirve para realizar predicciones más generales que se puedan verificar (en realidad no sirve para nada)
Chorradas parecidas nos podemos inventar muchas.
Ejemplo, nada existe, todo es producto de mi imaginación
Pues vale, no es demostrable ni rebatible. Tampoco es ciencia ni sirve para nada
Si pudiéramos hacer que el gato al abrir la caja estuviera vivo (por ejemplo) significaría que hemos forzado a que el átomo que lanzaría la radiacción, no la lance. Ahí tenemos dos efectos cuánticos conectados.
Lo malo es que nadie sabe como hacer que el gato esté vivo
Repetimos, esto no es ciencia, esto no sirve para nada
Pero a eso se parece la computación cuántica tan de moda
En caso de que se pudiera...
¿Cuál sería el esfuerzo necesario para interconectar cuánticamente 3 grupos de 32qbits en factores y resultado
¿Y 64qbits?
¿Merecería la pena?
Roger Penrose escribió un libro difícil que no entendí muy bien.
En este libro defendía la hipóteis de que el cerebro funcione con algoritmos cuánticos
Como no lo entendí, no me lo creo
Así se podría explicar porque los ordenadores son tan terriblemente torpes en cosas que son triviales para nosotros (incluso para un perro)
Hace meses, salió la fabulosa noticia del primer ordenador cuántico comercial del mundo con más de una decena de qbits
Desgraciadamente luego explicaron que cuántico, cuántico... que utilización de algoritmos cuánticos... no, pero era muy chulo
Pues nada, que sigan buscando el primer ordenador con algoritmos cuánticos y que me avisen cuando lo encuentren
jueves, abril 24, 2008
miércoles, abril 23, 2008
El algoritmo de ordenación MÁS EFICIENTE posible
Hacía tiempo que se conocía el peor algoritmo de ordenación posible y su coste, pero no se sabía cual podría ser ni el coste, ni mucho menos cómo podría ser el mejor algoritmo para ordenar (no mezclar, sin más consumo de memoria que la propia lista)
Un concienzudo estúdio teórico ha desvelado la respuesta a este problema nada trivial y ahora...
Ya se conoce el coste del mejor algoritmo de ordenación posible, y no sólo eso YA SE CONOCE EL MEJOR ALGORITMO DE ORDENACIÓN POSIBLE
Esto puede parecer trivial, pero es realmente un problema teórico enorme
No es el qsort ni variantes semejantes, es muchísimo mejor y revolucionario
El coste es O(n) pero todavía es teórico, no se ha conseguido llevar a la práctica
Hay varias universidades tratando de hacerlo efectivo
Consta de dos pasos muy sencillos de entender, pero el segundo paso, no ha sido resuelto
Es curioso porque está inspirado en el peor algoritmo de ordenación posible (que sí se conocía desde hace mucho tiempo)
Disfruta de esta revelación todavía poco popular, sé privilegiado...
bogo-sort: /boh`goh·sort´/, n.
http://www.catb.org/~esr/jargon/html/B/bogo-sort.html
Un concienzudo estúdio teórico ha desvelado la respuesta a este problema nada trivial y ahora...
Ya se conoce el coste del mejor algoritmo de ordenación posible, y no sólo eso YA SE CONOCE EL MEJOR ALGORITMO DE ORDENACIÓN POSIBLE
Esto puede parecer trivial, pero es realmente un problema teórico enorme
No es el qsort ni variantes semejantes, es muchísimo mejor y revolucionario
El coste es O(n) pero todavía es teórico, no se ha conseguido llevar a la práctica
Hay varias universidades tratando de hacerlo efectivo
Consta de dos pasos muy sencillos de entender, pero el segundo paso, no ha sido resuelto
Es curioso porque está inspirado en el peor algoritmo de ordenación posible (que sí se conocía desde hace mucho tiempo)
Disfruta de esta revelación todavía poco popular, sé privilegiado...
(var.: stupid-sort) The archetypical perversely awful algorithm (as opposed to bubble sort, which is merely the generic bad algorithm). Bogo-sort is equivalent to repeatedly throwing a deck of cards in the air, picking them up at random, and then testing whether they are in order. It serves as a sort of canonical example of awfulness. Looking at a program and seeing a dumb algorithm, one might say “Oh, I see, this program uses bogo-sort.” Esp. appropriate for algorithms with factorial or super-exponential running time in the average case and probabilistically infinite worst-case running time. Compare bogus, brute force.
A spectacular variant of bogo-sort has been proposed which has the interesting property that, if the Many Worlds interpretation of quantum mechanics is true, it can sort an arbitrarily large array in linear time. (In the Many-Worlds model, the result of any quantum action is to split the universe-before into a sheaf of universes-after, one for each possible way the state vector can collapse; in any one of the universes-after the result appears random.) The steps are: 1. Permute the array randomly using a quantum process, 2. If the array is not sorted, destroy the universe (checking that the list is sorted requires O(n) time). Implementation of step 2 is left as an exercise for the reader.
http://www.catb.org/~esr/jargon/html/B/bogo-sort.html
jueves, abril 17, 2008
Seguridad informática
O deberíamos decir INseguridad
http://historiasdequeso.blogspot.com/2008/04/usuarios-entregan-sus-contraseas-cambio.html
http://historiasdequeso.blogspot.com/2008/04/usuarios-entregan-sus-contraseas-cambio.html
Usuarios entregan sus contraseñas a cambio de ¿chocolate?
¿Quiere que un gusano llegue en forma de correo electrónico a la bandeja de entrada de alguien? Nada más sencillo, prométale una tableta de chocolate y todas sus contraseñas serán suyas.
Así lo aseguran los analistas de seguridad informática Infosecurity Europa, que encuestó a 576 trabajadores de oficinas de los alrededores de Liverpool Street, en Londres, como parte de su semana de concienciación sobre la seguridad de la información que comienza el 21 de Abril de este mismo año.
Según la encuesta, el 45% por ciento de las mujeres daban sus contraseñas a extraños con total tranquilidad a cambio de una tableta de chocolate, frente a sólo un 10% de los hombres. De haberles ofrecido cervezas gratis los resultados de la encuesta hubieran sido todavía más divertidos, si cabe. Para conseguirlo los de Infosecurity se hicieron pasar por analistas de mercado.
A los incautos se les pidió rellenar una encuesta que en realidad no era más que una tapadera para realizar la investigación sobre "ingeniería social" con tal de demostrar lo crédulos que podrían llegar a ser los usuarios, dando todo tipo de información privada a cambio de chocolate.
A pesar del gran numero de personas que picaron, Infosecurity estima que, en conjunto, la gente lo hizo mucho mejor que el año pasado cuando se realizó el mismo experimento. En el 2007 un tremendo 64 por ciento de personas estaban dispuestas a regalar sus contraseñas a cambio de una barra de chocolate con respecto al 21 por ciento que ha sucumbido a la tentación. Tal vez este año estén todos a dieta... xD. Pero aún así, las cifras son alarmantes.
El 61 por ciento no tuvieron ningún pudor a la hora de revelar su fecha de nacimiento, ni dudaron a la hora de dar la información personal de sus colegas, incluidos nombres, números de teléfono, solo para poder participar en un sorteo donde supuestamente podrían ganar un viaje a París. Paquetes de chocolate y París... no es de extrañar que el 60 por ciento de los hombres y el 62 por ciento de las mujeres dijeran "Si, quiero"
Infosecurity también descubrió que más de la mitad de las personas "encuestadas" utilizan una contraseña para todo, y que el 43 por ciento no la ha cambiado nunca. Un 58 por ciento entregó sus contraseñas cuando llamaron haciéndose pasar por el departamento de TI de su empresa, y la mitad afirmó conocer las contraseñas de sus colegas de oficina.
Claire Sellick, director de eventos de Infosecurity Europa dice que la promesa de un viaje podría costar muy cara a la gente, porque "una vez que un ciberdelincuente obtiene tu fecha de nacimiento, nombre y número de teléfono ya tiene toda la información necesaria para llevar a cabo ataques de "ingeniería social" más sofisticados hacía usted y posiblemente pretenda hacerse pasar por su banco o compañía de teléfonos para obtener más información valiosa que pueda ser utilizada para ejecutar algún fraude usando su identidad"
Cuando finalmente se les comunicó que la encuesta que acababan de rellenar era en realidad parte de una prueba para la semana de la concienciación sobre seguridad informática la mayoría se sorprendieron y algunos afirmaban que los investigadores parecían honestos y dignos de toda confianza.
Caos y Lorenz
Visto en Barrapunto
No sé si la historia es real, no he podido contrastarla, pero es un ejemplo interesante de caos.
Lorenz estaba haciendo simulaciones de tiempo atmosferico con ecuaciones diferenciales (totalmente deterministas) e iba viendo como variaban con el tiempo parametros como temperatura, presion atm, etc. Pero como en aquella epoca (70's) el tiempo de CPU estaba muy requerido, no tenía tiempo para hacer simulaciones largas completas. Entonces, cuando se acababa su tiempo, imprimia en un papel los valores de las variables y, cuando volvía a tener tiempo, introducía estos valores iniciales y continuaba la simulacion desde ahí. Entonces empezó a darse cuenta de que cuando repetía simulaciones que deberían ser exactas, los resultados variaban muchísimo. Al indagar en la causa, se dio cuenta de que se debía a que él imprimia los valores con unas pocas cifras decimales, mientras que el ordenador internamente consideraba más. Y esas diferencias en la 5a cifra decimal (consideradas totalmente despreciables) producían cambios drasticos (dependencia absoluta de los detalles de las condiciones iniciales, una caracteristica de los sistemas caóticos). Es decir, si el ordenador continuaba una simulación a partir de un valor de temperatura T=25.034256893823, y Lorenz continuaba otra a partir del valor que había impreso con menos decimales (T=25.03456899), las 2 simulaciones iban por derroteros totalmente diferentes. Cuando cualquiera hubiese esperado que fuesen igual o, al menos, trementamente parecidas (predicibilidad), ya que esa diferencia de temperatura (0.000000005) se pensaba era despreciable a todos los efectos.
Visto en Wikipedia...
La forma de mariposa del atractor de Lorenz puede haber inspirado el nombre del efecto mariposa en la Teoría del Caos.
No sé si la historia es real, no he podido contrastarla, pero es un ejemplo interesante de caos.
Lorenz estaba haciendo simulaciones de tiempo atmosferico con ecuaciones diferenciales (totalmente deterministas) e iba viendo como variaban con el tiempo parametros como temperatura, presion atm, etc. Pero como en aquella epoca (70's) el tiempo de CPU estaba muy requerido, no tenía tiempo para hacer simulaciones largas completas. Entonces, cuando se acababa su tiempo, imprimia en un papel los valores de las variables y, cuando volvía a tener tiempo, introducía estos valores iniciales y continuaba la simulacion desde ahí. Entonces empezó a darse cuenta de que cuando repetía simulaciones que deberían ser exactas, los resultados variaban muchísimo. Al indagar en la causa, se dio cuenta de que se debía a que él imprimia los valores con unas pocas cifras decimales, mientras que el ordenador internamente consideraba más. Y esas diferencias en la 5a cifra decimal (consideradas totalmente despreciables) producían cambios drasticos (dependencia absoluta de los detalles de las condiciones iniciales, una caracteristica de los sistemas caóticos). Es decir, si el ordenador continuaba una simulación a partir de un valor de temperatura T=25.034256893823, y Lorenz continuaba otra a partir del valor que había impreso con menos decimales (T=25.03456899), las 2 simulaciones iban por derroteros totalmente diferentes. Cuando cualquiera hubiese esperado que fuesen igual o, al menos, trementamente parecidas (predicibilidad), ya que esa diferencia de temperatura (0.000000005) se pensaba era despreciable a todos los efectos.
Visto en Wikipedia...
La forma de mariposa del atractor de Lorenz puede haber inspirado el nombre del efecto mariposa en la Teoría del Caos.
martes, abril 15, 2008
El famoso formato IEEE754
Este es el archiconocido formato para representar números en coma flotante.
No niego que sea un buen formato, pero es propenso a muchos errores. Tanto de técnicos como no técnicos.
Este formato no es un formato de números exactos, pero todos los lenguajes y sistemas que trabajan con él permiten hacer comparaciones de igualdad
Nunca lo he entendido.
Prueba en tu sistema favorito...
1*(0.5-0.4-0.1)
pensarás que es cero, ¿pero lo es en tu sistema?
(43.1-43.2)+1
pensarás que es 0.9 ¿pero que resultado da en tu sistema?
Lo que me ha sorprendido mucho es que OpenOffice hace las dos comparaciones correctamente, pero no el Excel
El problema, es viejo y conocido.
Un número representado exactamente en decimal, puede ser periódico en binario y viceversa
Entonces
¿PORQUÉ CARAJO LOS SISTEMAS PERMITEN COMPARAR COSAS QUE NO SON EXACTAS?
Y si lo hacen, al menos deberían tomarse las molestias de corregir esos defectos potenciales en la gran mayoría de casos como hace OpenOffice (y no hace Mocosoft Office)
Y además, los pobrecillos usarios de estos números pueden pensar que la suma es asociativa consigo misma y lo mismo para la multiplicación y división, pero no es así
No es necesariamente lo mismo...
(a+b)+c ~ a+(b+c)
(a*b)*c ~ a*(b*c)
Y mucho más evidente...
(a*b)/c /= a*(b/c)
Que los informáticos se tropiecen con esto... Pues que aprendan porque para eso son informáticos y deberían saberlo.
Pero es que esto también le toca las narices a los usuarios de hojas de cálculo como Excel.
En este caso gana por goleada OpenOffice, que se procupa por ser coherente con el usuario
No niego que sea un buen formato, pero es propenso a muchos errores. Tanto de técnicos como no técnicos.
Este formato no es un formato de números exactos, pero todos los lenguajes y sistemas que trabajan con él permiten hacer comparaciones de igualdad
Nunca lo he entendido.
Prueba en tu sistema favorito...
1*(0.5-0.4-0.1)
pensarás que es cero, ¿pero lo es en tu sistema?
(43.1-43.2)+1
pensarás que es 0.9 ¿pero que resultado da en tu sistema?
Lo que me ha sorprendido mucho es que OpenOffice hace las dos comparaciones correctamente, pero no el Excel
El problema, es viejo y conocido.
Un número representado exactamente en decimal, puede ser periódico en binario y viceversa
Entonces
¿PORQUÉ CARAJO LOS SISTEMAS PERMITEN COMPARAR COSAS QUE NO SON EXACTAS?
Y si lo hacen, al menos deberían tomarse las molestias de corregir esos defectos potenciales en la gran mayoría de casos como hace OpenOffice (y no hace Mocosoft Office)
Y además, los pobrecillos usarios de estos números pueden pensar que la suma es asociativa consigo misma y lo mismo para la multiplicación y división, pero no es así
No es necesariamente lo mismo...
(a+b)+c ~ a+(b+c)
(a*b)*c ~ a*(b*c)
Y mucho más evidente...
(a*b)/c /= a*(b/c)
Que los informáticos se tropiecen con esto... Pues que aprendan porque para eso son informáticos y deberían saberlo.
Pero es que esto también le toca las narices a los usuarios de hojas de cálculo como Excel.
En este caso gana por goleada OpenOffice, que se procupa por ser coherente con el usuario
jueves, marzo 27, 2008
Hilbert y su gran conferencia
http://www.historiasdelaciencia.com/?p=36
Hilbert, además, tenía salidas geniales. Un día le invitaron a dar una conferencia sobre el tema que él quisiera. La conferencia creó una gran expectación ya que el tema elegido fue : “La prueba del último teorema de Fermat”. Llegó el día y dio la conferencia. La exposición fue muy brillante pero no tuvo nada que ver con el último teorema de Fermat. Cuando le preguntaron el porqué del título contestó: “Oh, el título era solamente para el caso de que el avión se estrellara”.
Hilbert, además, tenía salidas geniales. Un día le invitaron a dar una conferencia sobre el tema que él quisiera. La conferencia creó una gran expectación ya que el tema elegido fue : “La prueba del último teorema de Fermat”. Llegó el día y dio la conferencia. La exposición fue muy brillante pero no tuvo nada que ver con el último teorema de Fermat. Cuando le preguntaron el porqué del título contestó: “Oh, el título era solamente para el caso de que el avión se estrellara”.
Inversión en ejecución concurrente Microsoft e Intel
Atención a la noticia...
http://www.infoq.com/news/2008/03/ParallelComputing
microsoft e intel invertirán 20millones de dólares para pensar como
hacer cosas que funcionen bien con muchos micropocesadores
1.- Ya hay una cosa fantástica y no han invertido tanto dinero Erlang
2.- Esto explica como escalan sus sistemas operativos (ver entrada anterior), de algún sitio
tienen que sacar el dinero
3.- Hablan de que el objetivo es chips con 1000 núcleos. Como
escarpias tengo los pelos de pensar lo que cuesta una licencia de
windows para ese chip tal y como escalan (nuevamente, ver entrada anterior)
Hace un par de días, el interesado era Java.
Vamos, que está de moda hablar de esto. Erlang lleva hablando del tema
muchos años.
curioso
pos ala, a comprar windows para 4 y 8 procesadores que necesitan
dinerito para invertir (en algo que ya existe, es libre y open source)
http://www.infoq.com/news/2008
microsoft e intel invertirán 20millones de dólares para pensar como
hacer cosas que funcionen bien con muchos micropocesadores
1.- Ya hay una cosa fantástica y no han invertido tanto dinero Erlang
2.- Esto explica como escalan sus sistemas operativos (ver entrada anterior), de algún sitio
tienen que sacar el dinero
3.- Hablan de que el objetivo es chips con 1000 núcleos. Como
escarpias tengo los pelos de pensar lo que cuesta una licencia de
windows para ese chip tal y como escalan (nuevamente, ver entrada anterior)
Hace un par de días, el interesado era Java.
Vamos, que está de moda hablar de esto. Erlang lleva hablando del tema
muchos años.
curioso
pos ala, a comprar windows para 4 y 8 procesadores que necesitan
dinerito para invertir (en algo que ya existe, es libre y open source)
Informática paralela
Ayer pude constatar algo que era más que probable, aunque no me guste
nada reconocerlo
No sé si te comenté algo de que la ley de Moore está agotada o cambiada.
Los procesadores ya no son más rápidos, ahora incorporan más núcleos
Hay documentación y gráficas por todos lados
¿Están los sistemas operativos, los programas y los lenguajes de
programación preparados para aprovechar sistemas con muchos
procesadores?
Hace poco Java se apuntó a esa corriente. Erlang es la mejor situada.
Haskell también está muy bien, etc...
Resulta que lo que mejor escala en el paralelismo NO ES ERLANG, ni
haskell, ni ada, ni la próxima versión de Java, ni Scala...
ES... microsoft
Cuando hay que reconocerlo se reconoce y punto
Para algo tenía que servir tantos cerebros concretrados en una empresa
La labor de ingeniería paralela realizada por los técnicos de
microsoft es aplastante y muy fácil de demostrar. Voy a ello...
Recordatorio...
Ahora que los procesadores no suben velocidad y suben en núcleos, que
ya no se pueden comprar mononúcleos y dentro de poco ni con dos
núcleos, es el momento y los sistemas operativos de microsoft están
ahí
Demostración...
Te compras una máquina con uno o dos procesadores, y le puedes poner
un XP Home o equivalente Vista. Precio... 120€
Pero si te la compras con tres o cuatro procesadores... Server básico.
Precio 1000€
Y si te hacen la faena de ponerte un par de procesadores multinúcleo y
el sistema operativo suma más de cuatro y menos de nueve... 3000€
Conclusión
Queda demostrado que en la informática paraLELAs y paraLELOs, lo que
mejor escala son lo sistemas operativos de mocosoft
Quiero pensar que mocosoft cambiará su estrategia a la VISTA de la
moda multicores, pero seguro que ellos también se beneficiarán del
cambio a costa de los paraLELOs y paraLELAs que no quieren poner linux
en casa
¿y GNU/LiNUX, que opina de todo esto?
Que yo sepan no escala bien, no creo que te cueste diferente para 2
que para 8 o 16 procesadores
nada reconocerlo
No sé si te comenté algo de que la ley de Moore está agotada o cambiada.
Los procesadores ya no son más rápidos, ahora incorporan más núcleos
Hay documentación y gráficas por todos lados
¿Están los sistemas operativos, los programas y los lenguajes de
programación preparados para aprovechar sistemas con muchos
procesadores?
Hace poco Java se apuntó a esa corriente. Erlang es la mejor situada.
Haskell también está muy bien, etc...
Resulta que lo que mejor escala en el paralelismo NO ES ERLANG, ni
haskell, ni ada, ni la próxima versión de Java, ni Scala...
ES... microsoft
Cuando hay que reconocerlo se reconoce y punto
Para algo tenía que servir tantos cerebros concretrados en una empresa
La labor de ingeniería paralela realizada por los técnicos de
microsoft es aplastante y muy fácil de demostrar. Voy a ello...
Recordatorio...
Ahora que los procesadores no suben velocidad y suben en núcleos, que
ya no se pueden comprar mononúcleos y dentro de poco ni con dos
núcleos, es el momento y los sistemas operativos de microsoft están
ahí
Demostración...
Te compras una máquina con uno o dos procesadores, y le puedes poner
un XP Home o equivalente Vista. Precio... 120€
Pero si te la compras con tres o cuatro procesadores... Server básico.
Precio 1000€
Y si te hacen la faena de ponerte un par de procesadores multinúcleo y
el sistema operativo suma más de cuatro y menos de nueve... 3000€
Conclusión
Queda demostrado que en la informática paraLELAs y paraLELOs, lo que
mejor escala son lo sistemas operativos de mocosoft
Quiero pensar que mocosoft cambiará su estrategia a la VISTA de la
moda multicores, pero seguro que ellos también se beneficiarán del
cambio a costa de los paraLELOs y paraLELAs que no quieren poner linux
en casa
¿y GNU/LiNUX, que opina de todo esto?
Que yo sepan no escala bien, no creo que te cueste diferente para 2
que para 8 o 16 procesadores
miércoles, marzo 26, 2008
Trabajando con sistemas críticos
Antes de empezar una aclaración.
NO PRETENDO DEMOSTRAR NADA EN ESTE CORREO.
Es frecuente que mucha gente utilice símiles para demostrar, pero eso es un error lógico total.
Los símiles sólo sirven para explicar.
Dicho esto...
Recordarás que el challenger explotó con 7 tripulantes a bordo.
Es más, había una importante expectación porque era la primera vez que había un tripulante civil (una profesora de colegio)
El tripulante civil, era claralmente una operación de marketing.
En un momento delicado, se pretendía demostrar que el transbordador era un gran invento.
Un camión de carga espacial, seguro y reutilizable.
El coste del trasbordador y los lanzamientos, eran bestiales
¿Estaba cumpliendo el carísimo transbordador la misión para la que fue desarrollado a un elevadísimo coste?
No.
Pero si se lanzaba con un civil, todo como si fuera una rutina y sin incidentes, podría parecer que casi.
Pero había algunos problemas.
Los ingenieros detectaron que había unas juntas tóricas (con forma de rosquilla) que tenían problemas.
Es más, sabían que tenían problemas gravísimos en condiciones de baja temperatura. No funcionaban como estaba previsto y las cosecuencias podían ser muy graves. (Para algo estarían estas juntas)
Un par de días antes del lanzamiento, un ingeniero jefe dijo que no de podría realizar.
La razón, es que tendrían una temperatura de un par de grados, y con ese frío, las juntas tóricas de los cohetes de combustible sólido...
Eso suponía para los gestores un revés importante.
Los gestores tenían la enorme responsabilidad de dar un empujon a la credibilidad y viabilidad de transbordador.
Pero los gestores no entendían nada de los argumentos de los ingenieros.
Así que cogieron al ingeniero jefe y lo presionaron para que firmara la aprobación para el lanzamiento.
Los gestores razonaron como sigue...
1.- Es importante realizar el lanzamiento según lo previsto
2.- Las juntas tóricas han tenido problemas en el pasado y todo fue bien. Lo que demuestra, que el sistema puede funcionar con este defecto en las juntas tóricas
3.- Los ingenieros son cobardes y excesivamente precavidos sin considerar en ningún momento otras cuestiones relevantes
El ingeniero firmó, por las presiones y considerando los argumentos de los gestores, por creer que quizá exageraba. El transbordador explotó matando a 7 personas
ERRORES EN RAZONAMIENTO DE LOS GESTORES
2.- Es un error lógico garrafal, deducir que algo no es importante porque no ha provocado un fallo en el pasado.
Eso no es científico, es un fallo muy grave que debe evitarse
Por dios, que nadie olvide que un defecto generá un fallo más tarde o temprano si le das las oportunidades suficientes. Es obvio
3.- Si no confías en la opinión de los ingenieros, no montes el sistema.
No olvidemos nunca que no sólo es importante la probablidad del fallo. Hay que valorar la unión de la probabilidad del fallo con el perjuicio del mismo
Otro símil clásico... Una pistola con 1 bala en un tambor de 6... tienes una probabilidad de pegarte un tiro en la ruleta rusa de 1/6. Es pequeña, ¿pero alguien en su sano juicio asumiría el riesgo?
No, porque no sólo es importante la probabilidad de que ocurra
Y ya sólo como curiosidad
En la comisión de investigación, detectaron más fallos importantes, empezando por dificultades burocráticas que incomunicaban ingenieros y mecánicos con gestores.
Fue difícil descubrir la causa, aunque había ingenieros muy afectados por lo ocurrido (ellos lo sabían)
Sólo se pudo indicar esta causa porque uno de los que formaban la comisión, era cabezota e intocable. Richard Feynman, premio de física en el 65 y uno de los mejores profesores de la historia
Dijo que si no se incluían sus observaciones, aunque fuera en un anexo, no firmaría y lo denunciaría en los medios de comunicación
CONCLUSIÓN...
¿APRENDIERON LA LECCIÓN?
SÍIIII
Ya sabes que hace poco, explotó en la reentrada otro transbordador
Este era un transbordador "reciclado".
Ya había terminado su vida útil según los ingenieros, pero eso es lo de menos.
Lo importante, es que explotó porque en el lanzamiento, el desprendimiento de un aislante blando y ligero del tanque central, provocó una avería en la nave.
TODOS SABÍAN QUE ERA FRECUENTE DESPRENDIMIENTOS DE ESTOS MATERIALES DURANTE EL LANZAMIENTO.
Y algunos pensaron... El que suceda desde el principio y con frecuencia, demuestra que no es peligroso. Nunca pasa nada.
¿Esto demuestra que yo no soy paranoico y pefeccionista?
NOOOOO
Pero espero que se entienda mejor mi punto de vista
Me considero no pefeccionista y podría detallar cientos de razones que lo avalan (de forma concreta en nuestro sistema).
Te sorprendería la cantidad de tornillos que están flojos en el sistema
El que se haya diseñado un sistema resistente a fallos, con ajuste continuo, no significa que pueda resistir cualquier cosa en todas condiciones.
El que defectos y fallos no provoquen incidentes graves, no demuestra que no sean importantes
¿De que sirve un sistema predictivo y dinámico si ignoramos sus advertencias y no realizamos los ajustes?
Antes de acusar de perfeccionismo hagamos un ejercicio...
¿Qué riesgos estáis dispuestos a asumir?
Valorad el coste de la reducción de esos riesgos con dichas situaciones
¿Cómo podéis acusarme por un lado de perfeccionista y por otro protestar (en muchas ocasiones) de que el sistema ha fallado por principio?
No es raro recibir llamadas que nos dicen... "el sistema ha funcionado mal Y ME HE PILLADO".
Luego cuesta horas, muchas horas, analizar lo sucedido y lo mismo para explicarlo. En el 99% de los casos, se demuestra que no ha sido un fallo del sistema.
No entiendo como en ocasiones culpamos al sistema por principio, para empezar, y por otro lado decimos que se trata de ser perfeccionista.
Es contradictorio
Pedazo reflexión (por el tamaño)
Si quieres más información del tema del challenger, hay un libro llamado "que le importa lo que digan los demás" que tiene el informe de Richard Feynman
(Yo aprendí muchas cosas de este informe)
saludos
Ejecución paralela en Java 7
Para Java 7, que está previsto que venga en el 2009
Comentarios...
Ya no son sólo los de la programación declarativa, especialmente Erlang los que dicen que hay que prestar atención a la ejecución paralela
Dan los mismos argumentos. La ley de Moore ha cambiado. Ahora los procesadores no son más rápidos, ahora incluyen más núcleos
Hablan de dividir los problemas recursivamente
De forma que los problemas más pequeños se puedan ejecutar en paralelo FORK
Y posteriormente combinar los resultados JOIN
Esta técnica la llaman FORK/JOIN
Para evitar la carga de la creación, destrucción y conmutación de threads, utilizan una piscina de threads donde distribuyen los trabajos.
El número de threads disponibles se ajustará al número de núcleos (más o menos)
Opinión subjetiva sin tener suficientes datos...
La idea parece chula y sencilla de utilizar, pero no confío que sea sencillo
Yo creo que este sistema, permitirá que algunos problemas se resuelvan de forma fácil y elegante.
Pero la mayoría de problemas, no serán triviales.
Es una mejora importante, quizá imprescindible, pero creo que utilizarla será un poco compleja y dificultará el diseño
Comprando con otros...
Erlang, está pensado desde el inicio para tabajar no sólo de forma concurrente, también de forma distribuida.
En erlang es natural tener muchos procesos (baratos) y además es muy fácil distribuir el programa. No es necesario pensar de otra forma
Scala
Probablemente Scala pueda aprovecharse mucho mejor de esta técnica que Java.
Si en Scala reduces la programación imperativa al mínimo y utilizas el modelo de actores (coordinación del paralelismo con paso de mensajes), el punto de partida es mucho mejor
Haskell
Como lenguaje declarativo, parte con una ventaja clara respecto a Java
pos eso
miércoles, marzo 19, 2008
El primer vuelo del Ariane-5
http://www.historiasdelaciencia.com/?p=249
El artículo de hoy está inspirado en uno que ya publicó Dan en su blog centpeus (blog en catalán) y del que ya os he hablado alguna vez, así que el mérito es enteramente de él. Yo, tan sólo, he retocado y añadido detalles.
La primera nave del Programa Mariner que llegó a Venus, el Mariner II, fue lanzada el 27 de agosto de 1962. Y si os preguntáis qué sucedió con el Mariner I os diré que cayó al mar inmediatamente después de despegar porque a alguien se le olvidó introducir un signo menos en el ordenador (dicen que fue un error al leerlo de la fórmula hecha a mano).
La NASA ha tenido bastantes fiascos posteriores debidos a fallos que podríamos calificar de “fácilmente evitables”. Uno de los mayores ridículos fue el perder una sonda que impactó contra la superficie de Marte porque se hicieron un lío entre una estación que expresaba las distancias en kilómetros y otra que lo hacía en millas.
Pero la ESA, la Agencia Espacial Europea, tampoco ha podido evitar unirse al espectáculo y el mayor y más sonado fue en el vuelo inicial del cohete Ariane-5, que estalló 39 segundos después del lanzamiento. Fue un golpe duro porque era el primer lanzamiento de la nueva generación de cohetes europeos, más grandes, más potentes y con más capacidad que los predecesores Ariane-4. El motivo del desastre fue ridículo: una de las unidades de 64 bits que controlaba la trayectoria hizo unos cálculos y emitió un número que envió a una unidad de 16 bits. Esta no pudo procesar el resultado porque el número era demasiado grande y simplemente ¡no cabía en 16 bits! Por lo tanto, hizo lo que hacen los ordenadores: dio un mensaje de error y se desconectó.
Había un sistema de emergencia que se puso en funcionamiento inmediatamente pero el software era idéntico al que había fallado, de forma que el error se repitió exactamente igual. La unidad también se desconectó, el cohete quedó sin control y adiós.
El problema con estas unidades fue que, en realidad aprovechaban el sistema operativo de los cohetes Ariane-4. Después de todo, aquel sistema había funcionado muy bien. Y si algo funciona correctamente lo mejor es no tocarlo (bien, esto es cierto a no ser que seas una multinacional de la informática que, por mantener el negocio, necesites vender cada 4 años un nuevo sistema operativo).
Pero, aun cuando el sistema iba muy bien por el Ariane-4, algunas cosas no servían para el Ariane-5 y esta era una de ellas.
La unidad que falló calculaba los desplazamientos horizontales del cohete y los técnicos no se debían preocupar por si daba un valor demasiado alto pues el Ariane-4 nunca se desplazaba tan deprisa. El problema era que el Ariane-5 era mucho más rápido y potente y sí que lo hacía. De forma que cuando el sistema detectó aquel desplazamiento lateral, no pudo calcularlo porque la realidad iba más allá de lo que en el diseño habían previsto (correctamente) que podía hacer un Ariane-4. En fin, que hizo que el ordenador central perdiera los datos de trayectoria del cohete y el desastre fue inevitable. La trayectoria no se pudo corregir de ninguna forma y al final empezó a ir demasiado “de lado”. Debido a esa inclinación (más de 20º), los propulsores se separaron de la etapa principal por efecto de las fuerzas aerodinámicas y se disparó el mecanismo de autodestrucción.
Y lo más irónico es que aquel sistema ya no hacía falta. La unidad que falló estaba diseñada por calcular los desplazamientos horizontales en los primeros segundos del lanzamiento, antes de que se estableciera el “modo de vuelo”, como si dijéramos cuando el cohete ya ha arrancado del todo.
Esto requería 40 segundos por los Ariane-4, pero sólo 3 segundos para el Ariane-5. De forma que el desastre pasó porque falló un procesador que, en realidad, ¡ya no servía para nada! Un curioso camino que empezó en un error al asumir que no hacía falta modificar el diseño de un programa informático y acabó en un fracaso de 7 mil millones de Euros.
Ya sabemos que no hay ningún sistema está 100% libre de errores pero, a veces, se pone de manifiesto de maneras bien espectaculares.
Moraleja: el “si funciona, no lo toques” no siempre es aplicable.
Fuentes:
“Astronomía”, Patrick Moore
http://centpeus.blogspot.com/2006/10/un-nmero-massa-gran.html
http://www.mononeurona.org/index.php?idnew=323
http://www.upv.es/satelite/trabajos/pract_9/kike/paginas/accid.htm
El Accidente del Columbia
http://es.geocities.com/fjcasadop/
El 1 de febrero de 2003, el telediario del mediodía nos sorprendía a muchos de nosotros con las imágenes, grabadas por un videoaficionado, del Columbia desintegrándose sobre el cielo de Texas, durante la maniobra de reentrada de la misión STS-107 del transbordador espacial norteamericano. El Columbia, el más veterano de la flota de transbordadores, contabilizaba con ésta un total de 28 misiones al espacio.
Casi de inmediato empezaron a surgir las primeras hipótesis sobre las causas del accidente, mostrándose unas imágenes tomadas durante el despegue de esta misión, en las que se observaba cómo un trozo del aislante que recubre gran el depósito central de propulsante se desprendía del mismo impactando sobre el ala izquierda del Columbia. Se planteaba que éste podía haber sido el origen del fallo, aunque al mismo tiempo se argumentaba que acontecimientos similares habían ocurrido en otros despegues sin que hubieran tenido el más mínimo efecto en la integridad del transbordador. De hecho, los técnicos de tierra habían observado el impacto y, tras varios días de debate, la conclusión oficial de la NASA era que no existía riesgo alguno, habiéndose proseguido la misión con normalidad.
Luego, como suele ocurrir, el accidente dejó de ser noticia, y la investigación sobre sus causas cayó en el olvido para el público en general.
Sin embargo, la investigación del accidente ha avanzado sin pausa en este tiempo, publicándose sus conclusiones el pasado mes de septiembre. El estudio ha sido exhaustivo: se han analizado uno a uno con gran detenimiento todos los datos (y son muchos) registrados por todos los sistemas de la nave a lo largo de la misión; se han observado una y otra vez los videos del despegue y las imágenes radar obtenidas durante la parte orbital de la misión; se han estudiado en detalle los restos minuciosamente recolectados a lo largo de varios estados; se han realizado múltiples ensayos de diferente tipo para intentar reproducir y validar las distintas hipótesis vertidas por el equipo de investigación sobre el desarrollo de los acontecimientos... Y como resultado de todo ello, la conclusión es que el desprendimiento y posterior impacto contra la parte inferior delantera del ala izquierda del transbordador de un trozo de espuma aislante desprendida del depósito ventral, fue el origen del daño que conduciría a la destrucción del vehículo durante la reentrada.
El trozo de aislante desprendido tenía una forma más o menos ovalada, con un tamaño de 500 a 700 mm de largo por 300 a 500 de ancho, y al menos 5 cm de espesor. Su peso estaba en torno a los 600 ó 800 gramos, y la velocidad de impacto fue del orden de los 260 m/s (más de 900 km/h) Aunque se trata de una ligerísima espuma rígida, los ensayos realizados durante la investigación han demostrado que, al contrario de lo que se pensó en su momento, un fragmento de estas características pudo llegar a ocasionar un gran agujero en el borde de ataque del ala izquierda del Columbia.
Se han estudiado otras posibilidades, como el impacto de un micrometeorito o de un fragmento de basura espacial durante la parte orbital de la misión, pero tras el detallado análisis de los sensores de la nave y las imágenes radar, no se ha encontrado nada que apoye esta hipótesis. No obstante, durante el segundo día en órbita se registró la separación de un pequeño objeto que se alejaba a baja velocidad de la nave. Tras extensos análisis, se ha descartado que pudiera proceder de algún equipo experimental de la bodega o que fuera algún deshecho del propio transbordador; se comparó la imagen radar obtenida de este objeto con la que dejarían distintos elementos de la nave, obteniéndose que sería aproximadamente idéntica a la que dejaría una loseta cerámica aislante del borde de ataque del ala, o una junta rígida de carbono del mismo borde de ataque. Aunque no puede probarse, parece probable que, tras el impacto, fragmentos del recubrimiento del borde de ataque cayeran hacia el interior del mismo, liberándose al exterior en ausencia de gravedad al efectuar una pequeña maniobra de giro del transbordador.
La secuencia del accidente se ha intentado reproducir y se conoce con bastante exactitud cómo se desarrollaron los acontecimientos. En un determinado momento de la maniobra de reentrada, con el Columbia ingresando en la atmósfera con el elevado ángulo de ataque requerido para presentar el escudo térmico en su posición más efectiva, comenzó a penetrar aire extremadamente caliente hacia el interior del ala a través de una fisura o, más probablemente, un agujero producido en el borde de ataque. Este flujo de gases a enorme temperatura fue erosionando y fundiendo los materiales, agrandando el agujero y avanzando por el interior del ala izquierda en dirección a la bahía del tren de aterrizaje. Los daños en el ala fueron aumentando, comenzando a afectar al elevón izquierdo y a la maniobrabilidad del transbordador, que empezó a desviarse de su actitud nominal en alabeo y guiñada. Los sistemas de control de la nave intentaron compensar la desviación, pero los daños fueron aumentando sin que pudiera restablecerse el control. Llegado un determinado momento, la posición del Columbia se alejó tanto de la nominal que el vehículo resultó destruido por las fuerzas aerodinámicas.
Fue, por tanto, el desprendimiento del aislante lo que provocó el accidente, pero ¿por qué se desprendió? ¿Fue una mala decisión del MRB, que aceptó con “use as is” un defecto en la aplicación del aislante que se había detectado en la inspección de calidad? ¿Se trató de un fallo aleatorio debido a la naturaleza misma del aislante y del procedimiento de aplicación? Probablemente nunca se sepa, pero las recomendaciones del comité investigador incluyen modificaciones en el esquema aislante del depósito central del transbordador espacial para evitar que hechos así se repitan en el futuro. Desprendimientos de aislante se han repetido en numerosos vuelos del transbordador espacial, pero nunca habían ocasionado ningún daño, y precisamente por ello no se le dio mayor importancia, aunque nunca hasta ahora el desprendimiento detectado había sido de esta magnitud.
De hecho, el informe del comité investigador es extremadamente crítico con la NASA, con su gestión y cultura interna, tanto en materia de seguridad como de organización en general. Es más, el comienzo y conclusiones del informe señala que si bien la causa física del accidente fue el desprendimiento del aislante, tan responsable o más que el propio trozo de aislante fue la gestión de la agencia en la valoración del incidente que dio lugar al trágico accidente con la pérdida de siete vidas.
Sin entrar en más detalle por la falta de espacio, simplemente señalar que los análisis advirtieron que existía la posibilidad de que el aislante hubiera podido penetrar en la estructura... aunque no era demostrable (el modelo no estaba preparado para impactos de esta magnitud). Para asegurarse, los técnicos pidieron que se tomasen imágenes del transbordador en órbita por parte de los sistemas ópticos del Dpto. de Defensa (telescopios espías de altísima resolución), pero la petición fue denegada por los gestores de la NASA, al considerar que no había motivos para la misma. El criterio general era que los habituales desprendimientos de espuma del depósito central no eran un asunto de seguridad de vuelo... aunque nunca se había probado lo contrario. La repetitividad de la anormalidad la había convertido en normalidad, sin ningún estudio que asegurase su inocuidad. De nuevo, como sucedió con el Challenger, el exceso de confianza y la priorización de los objetivos y plazos de la misión sobre la seguridad, tuvieron mucho que ver en este nuevo accidente de la aventura espacial.
El 1 de febrero de 2003, el telediario del mediodía nos sorprendía a muchos de nosotros con las imágenes, grabadas por un videoaficionado, del Columbia desintegrándose sobre el cielo de Texas, durante la maniobra de reentrada de la misión STS-107 del transbordador espacial norteamericano. El Columbia, el más veterano de la flota de transbordadores, contabilizaba con ésta un total de 28 misiones al espacio.
Casi de inmediato empezaron a surgir las primeras hipótesis sobre las causas del accidente, mostrándose unas imágenes tomadas durante el despegue de esta misión, en las que se observaba cómo un trozo del aislante que recubre gran el depósito central de propulsante se desprendía del mismo impactando sobre el ala izquierda del Columbia. Se planteaba que éste podía haber sido el origen del fallo, aunque al mismo tiempo se argumentaba que acontecimientos similares habían ocurrido en otros despegues sin que hubieran tenido el más mínimo efecto en la integridad del transbordador. De hecho, los técnicos de tierra habían observado el impacto y, tras varios días de debate, la conclusión oficial de la NASA era que no existía riesgo alguno, habiéndose proseguido la misión con normalidad.
Luego, como suele ocurrir, el accidente dejó de ser noticia, y la investigación sobre sus causas cayó en el olvido para el público en general.
Sin embargo, la investigación del accidente ha avanzado sin pausa en este tiempo, publicándose sus conclusiones el pasado mes de septiembre. El estudio ha sido exhaustivo: se han analizado uno a uno con gran detenimiento todos los datos (y son muchos) registrados por todos los sistemas de la nave a lo largo de la misión; se han observado una y otra vez los videos del despegue y las imágenes radar obtenidas durante la parte orbital de la misión; se han estudiado en detalle los restos minuciosamente recolectados a lo largo de varios estados; se han realizado múltiples ensayos de diferente tipo para intentar reproducir y validar las distintas hipótesis vertidas por el equipo de investigación sobre el desarrollo de los acontecimientos... Y como resultado de todo ello, la conclusión es que el desprendimiento y posterior impacto contra la parte inferior delantera del ala izquierda del transbordador de un trozo de espuma aislante desprendida del depósito ventral, fue el origen del daño que conduciría a la destrucción del vehículo durante la reentrada.
El trozo de aislante desprendido tenía una forma más o menos ovalada, con un tamaño de 500 a 700 mm de largo por 300 a 500 de ancho, y al menos 5 cm de espesor. Su peso estaba en torno a los 600 ó 800 gramos, y la velocidad de impacto fue del orden de los 260 m/s (más de 900 km/h) Aunque se trata de una ligerísima espuma rígida, los ensayos realizados durante la investigación han demostrado que, al contrario de lo que se pensó en su momento, un fragmento de estas características pudo llegar a ocasionar un gran agujero en el borde de ataque del ala izquierda del Columbia.
Se han estudiado otras posibilidades, como el impacto de un micrometeorito o de un fragmento de basura espacial durante la parte orbital de la misión, pero tras el detallado análisis de los sensores de la nave y las imágenes radar, no se ha encontrado nada que apoye esta hipótesis. No obstante, durante el segundo día en órbita se registró la separación de un pequeño objeto que se alejaba a baja velocidad de la nave. Tras extensos análisis, se ha descartado que pudiera proceder de algún equipo experimental de la bodega o que fuera algún deshecho del propio transbordador; se comparó la imagen radar obtenida de este objeto con la que dejarían distintos elementos de la nave, obteniéndose que sería aproximadamente idéntica a la que dejaría una loseta cerámica aislante del borde de ataque del ala, o una junta rígida de carbono del mismo borde de ataque. Aunque no puede probarse, parece probable que, tras el impacto, fragmentos del recubrimiento del borde de ataque cayeran hacia el interior del mismo, liberándose al exterior en ausencia de gravedad al efectuar una pequeña maniobra de giro del transbordador.
La secuencia del accidente se ha intentado reproducir y se conoce con bastante exactitud cómo se desarrollaron los acontecimientos. En un determinado momento de la maniobra de reentrada, con el Columbia ingresando en la atmósfera con el elevado ángulo de ataque requerido para presentar el escudo térmico en su posición más efectiva, comenzó a penetrar aire extremadamente caliente hacia el interior del ala a través de una fisura o, más probablemente, un agujero producido en el borde de ataque. Este flujo de gases a enorme temperatura fue erosionando y fundiendo los materiales, agrandando el agujero y avanzando por el interior del ala izquierda en dirección a la bahía del tren de aterrizaje. Los daños en el ala fueron aumentando, comenzando a afectar al elevón izquierdo y a la maniobrabilidad del transbordador, que empezó a desviarse de su actitud nominal en alabeo y guiñada. Los sistemas de control de la nave intentaron compensar la desviación, pero los daños fueron aumentando sin que pudiera restablecerse el control. Llegado un determinado momento, la posición del Columbia se alejó tanto de la nominal que el vehículo resultó destruido por las fuerzas aerodinámicas.
Fue, por tanto, el desprendimiento del aislante lo que provocó el accidente, pero ¿por qué se desprendió? ¿Fue una mala decisión del MRB, que aceptó con “use as is” un defecto en la aplicación del aislante que se había detectado en la inspección de calidad? ¿Se trató de un fallo aleatorio debido a la naturaleza misma del aislante y del procedimiento de aplicación? Probablemente nunca se sepa, pero las recomendaciones del comité investigador incluyen modificaciones en el esquema aislante del depósito central del transbordador espacial para evitar que hechos así se repitan en el futuro. Desprendimientos de aislante se han repetido en numerosos vuelos del transbordador espacial, pero nunca habían ocasionado ningún daño, y precisamente por ello no se le dio mayor importancia, aunque nunca hasta ahora el desprendimiento detectado había sido de esta magnitud.
De hecho, el informe del comité investigador es extremadamente crítico con la NASA, con su gestión y cultura interna, tanto en materia de seguridad como de organización en general. Es más, el comienzo y conclusiones del informe señala que si bien la causa física del accidente fue el desprendimiento del aislante, tan responsable o más que el propio trozo de aislante fue la gestión de la agencia en la valoración del incidente que dio lugar al trágico accidente con la pérdida de siete vidas.
Sin entrar en más detalle por la falta de espacio, simplemente señalar que los análisis advirtieron que existía la posibilidad de que el aislante hubiera podido penetrar en la estructura... aunque no era demostrable (el modelo no estaba preparado para impactos de esta magnitud). Para asegurarse, los técnicos pidieron que se tomasen imágenes del transbordador en órbita por parte de los sistemas ópticos del Dpto. de Defensa (telescopios espías de altísima resolución), pero la petición fue denegada por los gestores de la NASA, al considerar que no había motivos para la misma. El criterio general era que los habituales desprendimientos de espuma del depósito central no eran un asunto de seguridad de vuelo... aunque nunca se había probado lo contrario. La repetitividad de la anormalidad la había convertido en normalidad, sin ningún estudio que asegurase su inocuidad. De nuevo, como sucedió con el Challenger, el exceso de confianza y la priorización de los objetivos y plazos de la misión sobre la seguridad, tuvieron mucho que ver en este nuevo accidente de la aventura espacial.
Cuando los ingenieros se ponen en la piel de los gestores
http://www.historiasdelaciencia.com/?p=327
Sé que la historia de hoy la conocéis todos, pero no está de más desempolvar recuerdos para no olvidar errores de antaño. Uno de esos errores fue el desastre (que no accidente) del Challenger. Y sobre dicho desastre hablaremos en nuestra historia de hoy.
El 28 de enero de 1986, el excesivamente administrado programa espacial estadounidense alcanzó su nadir. Bajo la presión de tener que probar que el transbordador servía para lanzamientos sucesivos, funcionando como un camión, las administraciones de la NASA y de sus contratistas prefirieron ignorar las advertencias de los ingenieros.
El transbordador despegaba rumbo al espacio utilizando una combinación de cohetes; los motores de oxígeno e hidrógeno líquidos en la cola del orbitador y los dos cohetes aceleradores de combustible sólido, adosados a ambos lados del enorme depósito exterior que contenía el combustible líquido.
Los dos cohetes aceleradores de combustible sólido utilizados hasta 1986 eran una pila de segmentos reutilizables. Os pongo el detalle de uno de esos cohetes aceleradores.
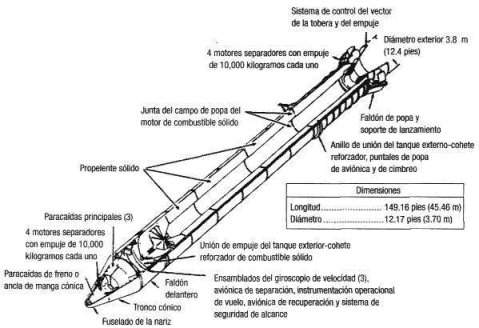
Después de cada vuelo, estas pilas se desmontaban, recargaban y volvían a montar. Las conexiones entre los segmentos se sellaban con dos juntas de goma, una principal y otra de apoyo, llamadas juntas tóricas (literalmente del ingés anillos-O).
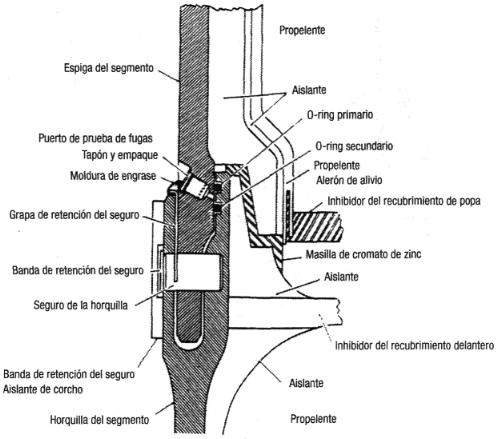
Para que dichas juntas funcionaran correctamente tenían que ser dúctiles y flexibles, capaces de cubrir bien la separación cuando el combustible comenzara a arder y la presión del gas lo empujara contra las conexiones entre los segmentos.
En siete de las nueve misiones que efectuaron los transbordadores en 1985 los ingenieros de Morthon Thiokol, la empresa fabricante de los cohetes aceleradores de combustible sólido, detectaron una erosión significativa y daños en las juntas tóricas primarias. En otro vuelo, realizado en abril de 1985, detectaron que una sección de una junta tórica primaria había quedado completamente calcinada. Estas pruebas sugerían que, en condiciones de bajas temperaturas, las juntas tóricas no funcionaban como se esperaba de su diseño. A pesar de la preocupación creciente entre los ingenieros, los transbordadores seguían volando. Tal y como Roger Boisjoly, ingeniero de Morthon Thiokol, escribió en un memorando fechado en julio de 1985: Siento el verdadero y sincero temor que si no actuamos inmediatamente y dedicamos un equipo a resolver el problema … entonces corremos el peligro de perder una misión junto con todas las instalaciones de lanzamiento.
En la mañana del 28 de enero de 1986, el pronóstico para cabo Cañaveral era de una temperatura de 2,2 ºC, próxima al punto de congelación. El transbordador Challenger se disponía a iniciar su décimo vuelo y la vigésimo quinta misión de los transbordadores. Transportaba a siete astronautas, entre ellos, la maestra de escuela Christa McAuliffe, que era el primer ciudadano estadounidense seleccionado para volar al espacio sin que formara parte del programa de astronautas de la NASA.
Los ingenieros de Morthon Thiokol volvieron a advertir a sus jefes y a los responsables de la NASA del Centro de Vuelo Espacial Marshall, quienes gestionaban las relaciones con el contratista, que las frías temperaturas de la Florida podían tener un efecto negativo sobre las juntas tóricas. Los gerentes, tanto en el centro Marshall como en Morthon Thiokol, se mostraban escépticos. Creían que los datos no eran concluyentes. Más importante aún: sentían la presión ineludible pero tácita de mantener el programa de vuelo previsto.
Siempre que la NASA había retrasado el lanzamiento de un transbordador, la agencia había tenido que enfrentarse al ridículo y a las acusaciones de sus adversarios en los medios de comunicación y el Congreso relativas a que el transbordador no estaba a la altura de la promesa de lanzamientos frecuentes y baratos. Esta presión pública la situaba en una posición incómoda: si se decantaba por la prudencia y cancelaba los lanzamientos bajo sospecha sería acusada de fracaso e incompetencia y daría municiones a aquellos adversarios que pretendían bajar el presupuesto de la agencia. Antes que brindarles a sus enemigos pruebas que el programa del transbordador era un fracaso, los administradores intentaban cada vez más a menudo aguantar el tipo, con la esperanza de demostrar que incluso en condiciones difíciles el transbordador podía funcionar como un avión de carga comercial.
La misma historia se repetía una y otra vez. Del mismo modo que las motivaciones políticas habían llevado a la NASA a comprometer tanto que el diseño del transbordador como el de la estación espacial, haciendo que ambos vehículos resultaran inadecuados para cumplir la tarea para la que habían sido originalmente concebidos, los gestores de Morthon Thiokol y de la NASA cambiaron una vez más de opinión en un intento inútil por complacer a los políticos, la prensa y el público; quienes o bien no comprendían el programa espacial o bien se oponían a él abiertamente.
En un momento de la noche anterior al lanzamiento, cuando los ingenieros de Morthon Thiokol intentaban desesperadamente convencer a sus jefes de que un lanzamiento al día siguiente podía ser muy arriesgado, un ejecutivo de la misma empresa, Jerald Mason, miró a Bob Lund, gerente del departamento de ingeniería y le dijo: “Bob, tienes que ponerte en la piel de un gestor y no en la de un ingeniero”.
La presión desde arriba, las dudas sobre los datos y la insistencia en que pensara “como un gestor y no como un ingeniero” fueron suficientes para que Lund cambiara de parecer. Se sumó a los otros gestores de Morthon Thiokol y, pasando por alto la opinión de sus ingenieros, certificó la seguridad de los cohetes aceleradores para el lanzamiento.
El Challenger despegó a las 11:38 de la mañana del 28 de enero de 1986. Sin embargo, tal y como temían Boisjoly y los demás ingenieros, al menos uno de las juntas tóricas del cohete acelerador de la derecha se había vuelto rígido y había perdido su flexibilidad a causa del frío. Con la junta incapaz de conservar el sellado hermético, un humo negro comenzó a filtrarse por la junta casi inmediatamente después de la ignición.
A los 58 segundos, cuando el transbordador había alcanzado una altura superior a los 6 km y se movía a una velocidad superior a la del sonido, las llamas producidas por la filtración comenzaron a extenderse al gigantesco depósito exterior. Antes del lanzamiento, este depósito contenía caso 630.000 L de oxígeno líquido y 1.700.000 L de hidrógeno líquido, la mayor parte de ellos todavía sin quemar en ese momento del vuelo. A los 74 segundos, se incendió el combustible del depósito y el transbordador, el depósito y los cohetes estallaron.
Los dos cohetes aceleradores salieron disparados como si fueran globos pinchados, obligando a los controladores de tierra a apretar sus botones de autodestrucción. El Challenger estalló en pedazos que se precipitaron al Atlántico. Su cabina de tripulantes, diseñada para resistir fuerzas como aquellas, resistió a la explosión y algunos de los tripulantes aún permanecían con vida en su interior.
Sin embargo, las fuerzas resultaron ser mortales; y el impacto contra el océano destruyó la cabina.
¿Hemos evolucionado desde entonces? Años después, en 1997, un astronauta estadounidense llamado Jerry Linenger estuvo un total de 132 días en la MIR. Fue el primer estadounidense en efectuar un paseo espacial vistiendo un traje ruso. Durante esa época tuvieron uno de sus momentos más críticos vividos en la MIR.
Al volver a la Tierra, cuestionó la seguridad de la estación y los gestores de la NASA se mostraron más proclives a calificarlo como “quejica” que a prestar atención a sus preocupaciones. Cuando Jim van Laak, el número dos del proyecto Shuttle-Mir escuchó el informe de Linenger, en vez de preocuparse, se enfureció. En lugar de dedicarse a investigar las quejas de Linenger, comenzó a controlar las entrevistas del astronauta con la prensa, al mismo tiempo que intentaba desacreditarle ante los periodistas. “En mi opinión Jerry Linenger no tiene razón”, comentó a los periodistas. También prohibió la circulación de transcripciones o notas de cualquier sesión informativa de dicho astronauta.
Nadie se levantó para afrontar los problemas comunicados por Linenger y decir: “Es difícil y hay cosas que han salido mal. Hemos cometido errores, pero todavía queremos hacerlo”. En vez de ello, todos se pusieron su gorra de gestor e hicieron como si los problemas no existiesen.
La situación no es muy esperanzadora. No hace falta que os diga que mintiendo no llegaremos muy lejos.
Volvamos con el Challenger. Tras el desastre, se formó la comisión Rogers. Uno de los componentes de dicha comisión fue Richard Feynman. Fue quien más duramente atacó la política de seguridad de la NASA. Les amenazó con retirar su firma del informe si no aparecían sus consideraciones personales, cuya última parte es famosa: para una gestión exitosa la realidad debe estar por delante de las relaciones públicas porque a la naturaleza no se la puede engañar. Bravo, Feynman.
Como ingeniero, me vais a permitir unas reflexiones. Estoy seguro que Bob Lund, el ingeniero al que presionaron “para que se pusiera en la piel de un gestor”, se sintió terriblemente responsable por ceder ante la presión. Sin embargo, sospecho que Mason, aquel ejecutivo que le presionó, se lavó las manos de cualquier responsabilidad, ya que él nunca tuvo que estampar su firma para garantizar la seguridad de los cohetes aceleradores y no era responsable de la seguridad de los mismos. Puede que su trabajo sólo consistiera en hacer presión o, simplemente, en transmitir la que le venía desde esferas más altas o una presión inventada por él mismo. Fuera su trabajo el que fuera, ¿cuál era exactamente su responsabilidad en el lanzamiento?
Pues bien, debo recordar a este ejecutivo y gentes que actúan de forma similar, que es muy fácil presionar a los ingenieros y a los técnicos: somos personas, y como tales, aguantaremos lo que haga falta. Llevadnos al límite de nuestro aguante, amenazadnos con despidos y ponednos en situaciones desesperadas. Lo conseguiréis: firmaremos, incluso, que un puente se mantiene con cuatro palillos. Ahora bien, debéis saber que los ingenieros no podemos presionar a la Naturaleza. No se deja. La Naturaleza no entiende de presiones políticas, económicas, personales, del público ni de la imagen. Es muy suya y tal y como Feynman lo sabía, lo sabemos también los ingenieros.
Es mucho más fácil presionar y responsabilizar a un técnico presionado de un error, que aguantar la presión y actuar con criterios de seguridad y de sentido común o, en caso de desastre, aceptar la responsabilidad de haber presionado. Es lo que se conoce coloquialmente como “endosar el marrón”: hazlo tú, hazlo para ayer y “mójate”; si sale bien, qué gran trabajo hemos hecho (algunos, incluso, dicen “gracias a mi gestión”); y si sale mal, el responsable eres tú.
Bien, amigo Jerald Mason. Ya has visto qué sucede cuando los ingenieros se ponen en la piel de los gestores. Ojalá llegue el día en que los gestores os pongáis en la piel de los ingenieros.
Conste que esta reflexión no la hubiera hecho si el Challenger hubiera explotado sin otras consecuencias más que las económicas o de imagen, al igual que sucedió con el Ariane-5. La reflexión es, sobre todo, porque hubo siete personas que pagaron con sus vidas toda esta lección de cómo no deben hacerse las cosas; personas que confiaron en el buen hacer de gestores y de ingenieros. Ojalá la lección haya sido asimilada, aunque me temo mucho que nunca aprenderemos.
Va por vosotros, muchachos.
Actualización: recomiendo leer el comentario de Javier Casado.
Fuentes:
“Adiós a la Tierra”, Robert Zimmerman
http://www.xtec.net/~cgarci38/ceta/tecnologia1/challenger.htm
Si queréis saber más sobre la catástrofe del Challenger y la comisión Rogers os recomiendo el libro Qué te importa lo que piensen los demás de Richard Feynman.
Tenéis montones de vídeos en youtube, por ejemplo, la explosión, el detalle de la cabina, etc.
miércoles, febrero 20, 2008
Observaciones Cpp
Observaciones Cpp
Puede que lo que voy a contar sea conocido en gran medida, pero seré breve y rápido.
Si alguien quiere repasar o profundizar en algún punto, fenomenal.
Los ejemplos no se han compilado e intencionadamente omito cosas que pueden hacer que no compilen (seguro que es obvio y no aporta nada escribirlo lo que falta)
Herencia
En c++ es normal hacer muchas cosas sin nada de herencia
No conviene abusar de la herencia
Algunos entendidos de c++ dicen que no se debe utilizar la herencia.
Excepto en casos que deben estar muy justificados
La herencia se utiliza con varios fines
Clasificación (es un)
Polimorfismo en tiempo de ejecución
Extender algo que ya existe
Constructor
Curiosa notación
// C++
class A {
int val;
A(int _val) : val(_val) {}
};
// Java
class A {
int val;
A(int _val)
{
val = _val;
}
};
¿Porqué en c++ se utiliza esa notación con ':'?
Son muy puristas
Les preocupa mucho el rendimiento
En el ejemplo anterior no hay una diferencia muy relevante.
En java, cuando se instancia una clase (se crea un objeto), la memoria que ocupará está rellenada con ceros. De esta forma todo se queda inicializado con los valores por defecto (quizá es por razones de seguridad).
Si luego le das un valor inicial, estás inicializando dos veces, una para nada.
Cuando se inicializan muchos objetos así, puede tener impacto en el rendimiento.
Pero en C++, se utiliza esta notación, sobre todo, por ser puristas y claros.
Un ejemplo más largo...
// C++
class A {
int entero;
A(int _entero) : entero(_entero) {}
};
class B {
A val; // #1
B(A valorInic) // esto no compila
{
val = valorInic;
}
};
No compila porque primero se crea val de tipo A con el contructor vacío (linea #1) y luego se intenta copiar el valor de valorInic en val.
Pero A no tiene constructor vacío.
En C++ el código del constructor, se ejecuta siempre, después de que se haya construído el objeto (en Java hay excepciones poco claras en la sintáxis)
Otro tipo de ejemplo...
// C++
class Padre {
int val;
Padre(int _val) : val(_val) {}
};
class Hija : public Padre {
Hija(int _val) // esto no compila
{
val = _val;
}
};
class Hija2 : public Padre {
Hija2(int _val) : Padre(_val) {} // ahora sí
};
Hija tampoco compila porque la clase padre no tiene constructor vacío.
Con la notación ':' se le dice que tiene que hacer en la construcción, no después
Destructores virtuales
Los destructores de C++ sólo son virtuales si se indica explícitamente
Que no sean virtuales les da más rendimiento, pero en ocasiones es necesario que sean virtuales
Ejemplo:
class Fruta {
int* punteroInt;
Fruta() : punteroInt(new int) {};
~Fruta() { delete punteroInt; };
};
class Platano : public Fruta {
int* punteroIntDelPlatano;
Platano() : punteroIntDelPlatano(new int) {};
~Platano() { delete punteroIntDelPlatano; };
};
...
Fruta* f = new Platano();
delete f;
En este mega programa tenemos una fuga de memoria (memoria sin liberar)
El tema es que f es de tipo de Fruta aunque señale a un plátano (como un plátano es una fruta...)
El delete f, llama al destructor de Fruta, con lo que se borra de la memoria su punteroInt. NUNCA SE LLAMA AL DESTRUCTOR del plátano (y este no tiene oportunidad de liberar su puntero, pobre....)
Una opción es hacer... delete dynamic_cast(f); (pero hay que estar un poco enfermo
Es mala opción porque no siempre sabes que f tiene un plátano, podría ser una fresa, y probar con todas las frutas es mala solución.
Opción 2. Hacer virtual el destructor del padre. SÍÍÍÍ
Opción 3. Pensárselo dos veces antes de utilizar la herencia y polimorfismo en tiempo de ejecución.
IMPORTANTE. Este problema no afecta sólo a la memoria, afecta a todo recurso "no local". Por ejemplo, un semáforo, región crítica, conexión bbdd, etc...
LA OPCIÓN CORRECTA... RAII
Tratar de no liberar explícitamente recursos (de ningun tipo)
Esto en el caso de la memoria, se puede hacer con un CountPtr
http://en.wikipedia.org/wiki/Resource_Acquisition_Is_Initialization)
Conviene saberlo aunque es poco probable que os suceda. Un escenario posible es con la vcl (haciendo algún componente)
Operador asignación y constructor de copia
C++ es muy amable y propone siempre que puede constructores de copia y operadores de asignación.
Pero no siempre los que propone sirven y hacen lo que queremos.
Es muy importante, siempre preguntarse si el que crea nos sirve o no
Anotar con un comentario que se ha verificado es saludable
OJO con clases con recursos no locales, habitualmente memoria en forma de punteros o referencias
Una curiosidad importante
class Pr {
Pr(int i)...
};
Pr prueba = Pr(4);
Aquí parece que...
Se instancia prueba de tipo Pr con constructor vacío
Luego se instancia Pr con valor 4
Luego se llama al operador de asignación para copiar el segundo objeto en el primero
PUES NO
Esa línea es totalmente equivalente a la siguiente (más clara en lo que hace)
Pr prueba(4);
Clases índice en mapas
std::map
Muy útil para almacenar datos indexados por lo que queramos de forma segura (verificación en tiempo de compilación) y eficiente
En un mapa la clase índice debe tener definida una relación de orden extricta con el operador <. Vamos, que si definimos el operador < style="font-weight: bold;">iteradores y end()
Por ejemplo, en un mapa llamamos al método find(xxx)
miMapa.find(esto)
SIEMPRE comprobar que no vale miMapa.end() (que significa que no lo ha encontrado)
En la próxima especificación de C++ esto será mejor
En Scala, en tiempo de compilación se verifica que no te olvidas
Si no se hace esta verificación, el programa explotará en algunas ocasiones
Punteros y referencias
No utilizar punteros crudos ni aritmética de punteros
Las referencias son punteros que no lo parecen (indirección implícita) y que siempre tienen valor (siempre están inicializados) y no tienen aritmética de punteros
Punteros nunca, referencias sí, en muchos casos
Envíe "aunque parezca increíble estoy leyendo esto" al 555 55 55, participará en el sorteo de un concepto
Los punteros a punteros y punteros a referencias NOOOOOOOO, caca, caca
Fugas de memoria
Dicen que C y C++ padecen de esto, pero... no parece razonable para el caso de C++
Para los casos raros en los que es necesario un puntero (memoria de montículo o por polimorfismo en tiempo de ejecución), utiliza un CountPtr
El problema del CountPtr está en las referencias circulares, pero no es tan fácil diseñar algo con referencias circulares en C++, especialmente si no se abusan de los punteros.
Con muy poco cuidado, eso no pasará nunca
Multimétodos
C++ no tiene
Está de moda, pero no hay consenso y lo discuten mucho
Scala, que ha metido de todo, no los tiene. El autor inicialmente dijo que no se acordó, pero después no lo puso porque decía era mejor sin.
Hay discusiones sobre esto en internet
A pesar de ser un concepto sencillo, tarde bastante en enterarme
// sin multimétodos
class Grafo {
virtual Distancia(Punto punto)=0;
}
class Punto : public Grafo
{
Distancia (Punto punto);
}
class Linea : public Grafo
{
Distancia (Punto punto);
}
Grafo g1 = new Punto(100,200);
Grafo g2 = new Punto(200, 600);
g1.Distancia(Punto(120, 400));
Grafo g3(100, 250, 30);
g3.Distancia(Punto(120, 400));
// con multimétodos
class Grafo {
...
}
class Punto : public Grafo
{
...
}
class Linea : public Grafo
{
...
}
Distancia(Punto p1, Punto p2) ...
Distancia(Linea l1, Punto p1) ...
Distancia(Linea l1, Linea l2) ...
Grafo g1 = new Punto(100,200);
Grafo g2 = new Punto(200, 600);
Grafo g3(100, 250, 30);
Distancia(g1, g2);
Distancia(g3, g2);
Sin multimétodos, la llamada a Distancia del un objeto Grafo, se pasa en tiempo de ejecución al hijo que corresponda, un punto o una línea (polimorfismo en tiempo de ejecución, una de las claves fundamentales de la OOP)
Pero el segundo objeto sobre el que se realiza el cálculo (el parámetro), no puede utilizar el mismo truco
Con multimétodos, a pesar de que llamamos a Distancia con dos parámetros de tipo Grafo, y no existe una Distancia definida para dos Grafos, en tiempo de ejecución, verifica que uno de los parámetros concretamente es un punto y el otro una línea y llama a esa Distancia concreta (o la que corresponda)
Se parece al polimorfismo en tiempo de ejecución, pero no sólo para uno, sino para varios
Lo dicho, que hay una discusión sobre el tema que se puede ver en internet
No está en C++ ni estará en la próxima especificación
Herencia múltiple de implementación
No utilizar
Es cierto que en algunos casos puede ser muy interesante, pero es muy delicado
Ahora está más de moda (y parece mejor) los mixins
Conversión implícita
Es un recurso potente que debe utilizarse con cuidado
Se puede conseguir en varias direcciones
Un constructor con un sólo parámetro del tipo a convertir
Operadores en la clase que se convierte
Podéis ver un ejemplo en la clase Variant de jleTibco
En general no utilizar
NUNCA...
NUNCA Utilizaré aritmética de punteros
NUNCA Utilizaré punteros crudos
NUNCA Arrays al estilo C (que en el fondo son punteros con aritmética de punteros)
En su lugar std::vector
NUNCA Herencia múltiple de implementación
NUNCA Abusaré de la herencia
NUNCA Utilizaré dynamic_cast, const_cast, ... (RTTI)
NUNCA Utilizaré reinterpret_cast (nunca jamás)
NUNCA haré un casting al estilo C (nunca jamás)
NUNCA Haré piezas que requieran liberación explícita de recursos
NUNCA Haré programas con muchas hebras
NUNCA Utilizaré mecanismos de concurrencia de bajo nivel (regiones críticas, semáforos, monitores, etc...)
NUNCA utilizaré "using namespace"
NUNCA intentaré utilizar namespaces anidados
NUNCA diré en la definición de una función o método las excepciones que puede lanzar
NUNCA pondré un nombre a un namespace superior a 3 letras
NUNCA utilizaré macros
NUNCA pensaré que C++ se parece a C
NUNCA manejaré los string de C ni la entrada salida de C, ni lista de parámetros variables (C otra vez)
NUNCA utilizar malloc ni semejantes
NUNCA Pondré degradados de colores ;-P
(consejos de un pecador)
Puede que lo que voy a contar sea conocido en gran medida, pero seré breve y rápido.
Si alguien quiere repasar o profundizar en algún punto, fenomenal.
Los ejemplos no se han compilado e intencionadamente omito cosas que pueden hacer que no compilen (seguro que es obvio y no aporta nada escribirlo lo que falta)
Herencia
En c++ es normal hacer muchas cosas sin nada de herencia
No conviene abusar de la herencia
Algunos entendidos de c++ dicen que no se debe utilizar la herencia.
Excepto en casos que deben estar muy justificados
La herencia se utiliza con varios fines
Clasificación (es un)
Polimorfismo en tiempo de ejecución
Extender algo que ya existe
Constructor
Curiosa notación
// C++
class A {
int val;
A(int _val) : val(_val) {}
};
// Java
class A {
int val;
A(int _val)
{
val = _val;
}
};
¿Porqué en c++ se utiliza esa notación con ':'?
Son muy puristas
Les preocupa mucho el rendimiento
En el ejemplo anterior no hay una diferencia muy relevante.
En java, cuando se instancia una clase (se crea un objeto), la memoria que ocupará está rellenada con ceros. De esta forma todo se queda inicializado con los valores por defecto (quizá es por razones de seguridad).
Si luego le das un valor inicial, estás inicializando dos veces, una para nada.
Cuando se inicializan muchos objetos así, puede tener impacto en el rendimiento.
Pero en C++, se utiliza esta notación, sobre todo, por ser puristas y claros.
Un ejemplo más largo...
// C++
class A {
int entero;
A(int _entero) : entero(_entero) {}
};
class B {
A val; // #1
B(A valorInic) // esto no compila
{
val = valorInic;
}
};
No compila porque primero se crea val de tipo A con el contructor vacío (linea #1) y luego se intenta copiar el valor de valorInic en val.
Pero A no tiene constructor vacío.
En C++ el código del constructor, se ejecuta siempre, después de que se haya construído el objeto (en Java hay excepciones poco claras en la sintáxis)
Otro tipo de ejemplo...
// C++
class Padre {
int val;
Padre(int _val) : val(_val) {}
};
class Hija : public Padre {
Hija(int _val) // esto no compila
{
val = _val;
}
};
class Hija2 : public Padre {
Hija2(int _val) : Padre(_val) {} // ahora sí
};
Hija tampoco compila porque la clase padre no tiene constructor vacío.
Con la notación ':' se le dice que tiene que hacer en la construcción, no después
Destructores virtuales
Los destructores de C++ sólo son virtuales si se indica explícitamente
Que no sean virtuales les da más rendimiento, pero en ocasiones es necesario que sean virtuales
Ejemplo:
class Fruta {
int* punteroInt;
Fruta() : punteroInt(new int) {};
~Fruta() { delete punteroInt; };
};
class Platano : public Fruta {
int* punteroIntDelPlatano;
Platano() : punteroIntDelPlatano(new int) {};
~Platano() { delete punteroIntDelPlatano; };
};
...
Fruta* f = new Platano();
delete f;
En este mega programa tenemos una fuga de memoria (memoria sin liberar)
El tema es que f es de tipo de Fruta aunque señale a un plátano (como un plátano es una fruta...)
El delete f, llama al destructor de Fruta, con lo que se borra de la memoria su punteroInt. NUNCA SE LLAMA AL DESTRUCTOR del plátano (y este no tiene oportunidad de liberar su puntero, pobre....)
Una opción es hacer... delete dynamic_cast
Es mala opción porque no siempre sabes que f tiene un plátano, podría ser una fresa, y probar con todas las frutas es mala solución.
Opción 2. Hacer virtual el destructor del padre. SÍÍÍÍ
Opción 3. Pensárselo dos veces antes de utilizar la herencia y polimorfismo en tiempo de ejecución.
IMPORTANTE. Este problema no afecta sólo a la memoria, afecta a todo recurso "no local". Por ejemplo, un semáforo, región crítica, conexión bbdd, etc...
LA OPCIÓN CORRECTA... RAII
Tratar de no liberar explícitamente recursos (de ningun tipo)
Esto en el caso de la memoria, se puede hacer con un CountPtr
http://en.wikipedia.org/wiki/Resource_Acquisition_Is_Initialization)
Conviene saberlo aunque es poco probable que os suceda. Un escenario posible es con la vcl (haciendo algún componente)
Operador asignación y constructor de copia
C++ es muy amable y propone siempre que puede constructores de copia y operadores de asignación.
Pero no siempre los que propone sirven y hacen lo que queremos.
Es muy importante, siempre preguntarse si el que crea nos sirve o no
Anotar con un comentario que se ha verificado es saludable
OJO con clases con recursos no locales, habitualmente memoria en forma de punteros o referencias
Una curiosidad importante
class Pr {
Pr(int i)...
};
Pr prueba = Pr(4);
Aquí parece que...
Se instancia prueba de tipo Pr con constructor vacío
Luego se instancia Pr con valor 4
Luego se llama al operador de asignación para copiar el segundo objeto en el primero
PUES NO
Esa línea es totalmente equivalente a la siguiente (más clara en lo que hace)
Pr prueba(4);
Clases índice en mapas
std::map
Muy útil para almacenar datos indexados por lo que queramos de forma segura (verificación en tiempo de compilación) y eficiente
En un mapa la clase índice debe tener definida una relación de orden extricta con el operador <. Vamos, que si definimos el operador < style="font-weight: bold;">iteradores y end()
Por ejemplo, en un mapa llamamos al método find(xxx)
miMapa.find(esto)
SIEMPRE comprobar que no vale miMapa.end() (que significa que no lo ha encontrado)
En la próxima especificación de C++ esto será mejor
En Scala, en tiempo de compilación se verifica que no te olvidas
Si no se hace esta verificación, el programa explotará en algunas ocasiones
Punteros y referencias
No utilizar punteros crudos ni aritmética de punteros
Las referencias son punteros que no lo parecen (indirección implícita) y que siempre tienen valor (siempre están inicializados) y no tienen aritmética de punteros
Punteros nunca, referencias sí, en muchos casos
Envíe "aunque parezca increíble estoy leyendo esto" al 555 55 55, participará en el sorteo de un concepto
Los punteros a punteros y punteros a referencias NOOOOOOOO, caca, caca
Fugas de memoria
Dicen que C y C++ padecen de esto, pero... no parece razonable para el caso de C++
Para los casos raros en los que es necesario un puntero (memoria de montículo o por polimorfismo en tiempo de ejecución), utiliza un CountPtr
El problema del CountPtr está en las referencias circulares, pero no es tan fácil diseñar algo con referencias circulares en C++, especialmente si no se abusan de los punteros.
Con muy poco cuidado, eso no pasará nunca
Multimétodos
C++ no tiene
Está de moda, pero no hay consenso y lo discuten mucho
Scala, que ha metido de todo, no los tiene. El autor inicialmente dijo que no se acordó, pero después no lo puso porque decía era mejor sin.
Hay discusiones sobre esto en internet
A pesar de ser un concepto sencillo, tarde bastante en enterarme
// sin multimétodos
class Grafo {
virtual Distancia(Punto punto)=0;
}
class Punto : public Grafo
{
Distancia (Punto punto);
}
class Linea : public Grafo
{
Distancia (Punto punto);
}
Grafo g1 = new Punto(100,200);
Grafo g2 = new Punto(200, 600);
g1.Distancia(Punto(120, 400));
Grafo g3(100, 250, 30);
g3.Distancia(Punto(120, 400));
// con multimétodos
class Grafo {
...
}
class Punto : public Grafo
{
...
}
class Linea : public Grafo
{
...
}
Distancia(Punto p1, Punto p2) ...
Distancia(Linea l1, Punto p1) ...
Distancia(Linea l1, Linea l2) ...
Grafo g1 = new Punto(100,200);
Grafo g2 = new Punto(200, 600);
Grafo g3(100, 250, 30);
Distancia(g1, g2);
Distancia(g3, g2);
Sin multimétodos, la llamada a Distancia del un objeto Grafo, se pasa en tiempo de ejecución al hijo que corresponda, un punto o una línea (polimorfismo en tiempo de ejecución, una de las claves fundamentales de la OOP)
Pero el segundo objeto sobre el que se realiza el cálculo (el parámetro), no puede utilizar el mismo truco
Con multimétodos, a pesar de que llamamos a Distancia con dos parámetros de tipo Grafo, y no existe una Distancia definida para dos Grafos, en tiempo de ejecución, verifica que uno de los parámetros concretamente es un punto y el otro una línea y llama a esa Distancia concreta (o la que corresponda)
Se parece al polimorfismo en tiempo de ejecución, pero no sólo para uno, sino para varios
Lo dicho, que hay una discusión sobre el tema que se puede ver en internet
No está en C++ ni estará en la próxima especificación
Herencia múltiple de implementación
No utilizar
Es cierto que en algunos casos puede ser muy interesante, pero es muy delicado
Ahora está más de moda (y parece mejor) los mixins
Conversión implícita
Es un recurso potente que debe utilizarse con cuidado
Se puede conseguir en varias direcciones
Un constructor con un sólo parámetro del tipo a convertir
Operadores en la clase que se convierte
Podéis ver un ejemplo en la clase Variant de jleTibco
En general no utilizar
NUNCA...
NUNCA Utilizaré aritmética de punteros
NUNCA Utilizaré punteros crudos
NUNCA Arrays al estilo C (que en el fondo son punteros con aritmética de punteros)
En su lugar std::vector
NUNCA Herencia múltiple de implementación
NUNCA Abusaré de la herencia
NUNCA Utilizaré dynamic_cast, const_cast, ... (RTTI)
NUNCA Utilizaré reinterpret_cast (nunca jamás)
NUNCA haré un casting al estilo C (nunca jamás)
NUNCA Haré piezas que requieran liberación explícita de recursos
NUNCA Haré programas con muchas hebras
NUNCA Utilizaré mecanismos de concurrencia de bajo nivel (regiones críticas, semáforos, monitores, etc...)
NUNCA utilizaré "using namespace"
NUNCA intentaré utilizar namespaces anidados
NUNCA diré en la definición de una función o método las excepciones que puede lanzar
NUNCA pondré un nombre a un namespace superior a 3 letras
NUNCA utilizaré macros
NUNCA pensaré que C++ se parece a C
NUNCA manejaré los string de C ni la entrada salida de C, ni lista de parámetros variables (C otra vez)
NUNCA utilizar malloc ni semejantes
NUNCA Pondré degradados de colores ;-P
(consejos de un pecador)
domingo, febrero 17, 2008
programación imperativa vs declarativa
Programación imperativa vs declarativa
Yo no soy expecialista en programación declarativa.
Una visión global y breve...
Conceptos breves antes de empezar...
La característica fundamental de la programación declarativa es que no tiene asignación destructiva. Es decir, que una variable no puede cambiar su valor.
Esto provoca que el orden de ejecución no tiene porque ser secuencial.
Los bucles hay que reemplazarlos por funciones recursivas.
1.---------------------------------------------------------------
Existen problemas que son naturalmente imperativos.
Un programa se descompone en entrada, proceso y salida.
Tanto la entrada como la salida, son acciones imperativas (consola, conexión tcp, fichero, etc..).
La mayoría de lenguajes declarativos, tienen características imperativas para ello (no son declarativos puros)
2.---------------------------------------------------------------
Todos los programadores declarativos conocen la programación imperativa.
Lógicamente, esto es porque la programación imperativa está muchísimo más extendida
Casi todos los programadores declarativos, empezaron con la programación imperativa, y ahora defienden la programación declarativa sobre la imperativa.
Esto podría ser el famoso efecto de las minorías y débiles, que tratan de compensarlo gritando más.
Pero en este caso, lo argumentan con lógica.
Richard Stallman, un genio de la programación, eligió LISP para su proyecto estrella Emacs
c omega es el lenguaje de programación para experimentar novedades para c#.
Inicialmente, este lenguaje se obtenía modificando el compilador de c# (que está escrito en c++ ¿no es tan bueno c#?).
Pero los programadores dijeron que era muy duro andar tocando el compilador c++ y optaron por utilizar un dialecto de scheme que generaba código c#, que luego volvían a compilar.
Aquí hay un tutorial de haskell para programadores imperativos
http://www.haskell.org/~pairwise/intro/intro.html
3.---------------------------------------------------------------
En la programación declarativa es más fácil la verificación de los programas.
En programación imperativa no sólo importa los valores con los que se llaman, también depende el orden de la llamada al método, a los métodos del objeto y casi siempre, a cualquier cosa del programa. Esto provoca una explosión de posibilidades imposible de verificar.
4.---------------------------------------------------------------
Los lenguajes declarativos suelen tener un poder expresivo impresionante.
El caso más radical es Haskell. Probablemente el lenguaje más potente y expresivo.
Quizá para ser capaz de sacarle partido, es necesaria una capacidad especial.
5.---------------------------------------------------------------
Los lenguajes declarativos, especialmente Haskell tienen fama de no ser muy eficientes.
Creo que para ejemplos sencillos, que se pueden optimizar fácilmente en c/c++ (por ejemplo), Haskell puede estar detrás.
Pero para casos reales, grandes y complejos de optimizar, Haskell tiene ventajas importantes.
La evaluación perezosa, la optimización dinámica y que el compilador pueda elegir el orden de ejecución para buscar el más óptimo... seguramente produzcan un código muy eficiente, sin mucha preocupación al programador.
Sin estas herramientas, todos sabemos, que las optimizaciones son la principal fuente de errores en los programas.
6.---------------------------------------------------------------
Los lenguajes declarativos son naturalmente paralelizables
Aquí la diferencia es radical e incomparable.
Un ejemplo muy bueno está en el lenguaje Erlang.
Erlang es un lenguaje declarativo muy, muy sencillo (uno de los más sencillos que he visto en mi vida)
Está orientado a sistemas de ejecución paralela, distribuida, tolerante a fallos, ejecución continua...
Para el SO, crear un proceso es caro, conmutar un proceso es caro.
Es más barato con hebras (para eso se crearon), pero aún así sigue siendo un recurso caro (unos pocos miles es demasiado).
En Erlang, crear un proceso es increíblemente barato, y lo mismo para las conmutaciones, y lo mismo para el paso de mensajes (nada de numeritos, mensajes complejos)
Ejemplo en yaws (yet another web server). Comparación con apache.
http://www.sics.se/~joe/apachevsyaws.html
Esta comparación es salvaje, pero también es comparar dos productos en el punto fuerte de uno de ellos.
En 4000 peticiones simultáneas, Apache casca, demasiados procesos.
Mientas que yaws (erlang) da mejor rendimiento incluso para 80.000 peticiones simultáneas.
7.---------------------------------------------------------------
El futuro es la programación paralela, dicen algunos.
La velocidad de los micros se ha parado, ahora buscan potencia haciéndolos multinúcleo.
Intel dice que prevee meter hasta 100 núcleos.
¿Están los programas preparados para aprovechar estas nuevas configuraciones?
NO
¿Están los lenguajes de programación preparados para ayudar en este nuevo escenario?
Los imperativos no.
Aquí tenéis un artículo fantástico
http://www.gotw.ca/publications/concurrency-ddj.htm
8.---------------------------------------------------------------
La programación declarativa es extrictamente académica??
Seguro que no está tan difundida como la imperativa, pero muchos defienden que no es puramente académica.
Se utilizar en las universidades, por profesores e investigadores, porque probablemente es la mejor opción.
Erlang está funcionando en máquinas muy caras con unas cifras espectaculares.
Ericson está explotando Erlang en máquinas con programas de más de 3 millones de líneas de código, con una tasa de fallo de 31 milisegundos al año
http://www.erlang.se/publications/BYTE2003.html
9.---------------------------------------------------------------
La programación declarativa es mejor para cosas pequeñas.
Erlang ha demostrado que puede funcionar muy bien en proyectos enormes.
Exprogramadores imperativos dicen que la gran ventaja de Haskell es para programas grandes o enormes
http://www.haskell.org/~pairwise/intro/intro.html
Scala recomienda utilizar todo lo posible la programación declarativa para poder eSCALAr al máximo.
10.-------------------------------------------------------------
Gran parte de las novedades de los lenguajes imperativos, o son características declarativas, o son cosas que aparecieron antes en estos lenguajes.
11.-------------------------------------------------------------
Líneas de código, tiempo de desarrollo...
Algunas pruebas dicen que Haskell gana
http://www.haskell.org/papers/NSWC/jfp.ps
12.-------------------------------------------------------------
Un inconveniente con los lenguajes muy expresivos, es que hace difícil la vida a los IDE y los compiladores.
Para un IDE es mucho más difícil funciones como autocompletar.
Para un compilador es más difícil informar con precisión del error.
Ver caso de C++ (seguro que también le sucederá a Scala). Creo que le pasa a Haskell
Yo no soy expecialista en programación declarativa.
Una visión global y breve...
Conceptos breves antes de empezar...
La característica fundamental de la programación declarativa es que no tiene asignación destructiva. Es decir, que una variable no puede cambiar su valor.
Esto provoca que el orden de ejecución no tiene porque ser secuencial.
Los bucles hay que reemplazarlos por funciones recursivas.
1.---------------------------------------------------------------
Existen problemas que son naturalmente imperativos.
Un programa se descompone en entrada, proceso y salida.
Tanto la entrada como la salida, son acciones imperativas (consola, conexión tcp, fichero, etc..).
La mayoría de lenguajes declarativos, tienen características imperativas para ello (no son declarativos puros)
2.---------------------------------------------------------------
Todos los programadores declarativos conocen la programación imperativa.
Lógicamente, esto es porque la programación imperativa está muchísimo más extendida
Casi todos los programadores declarativos, empezaron con la programación imperativa, y ahora defienden la programación declarativa sobre la imperativa.
Esto podría ser el famoso efecto de las minorías y débiles, que tratan de compensarlo gritando más.
Pero en este caso, lo argumentan con lógica.
Richard Stallman, un genio de la programación, eligió LISP para su proyecto estrella Emacs
c omega es el lenguaje de programación para experimentar novedades para c#.
Inicialmente, este lenguaje se obtenía modificando el compilador de c# (que está escrito en c++ ¿no es tan bueno c#?).
Pero los programadores dijeron que era muy duro andar tocando el compilador c++ y optaron por utilizar un dialecto de scheme que generaba código c#, que luego volvían a compilar.
Aquí hay un tutorial de haskell para programadores imperativos
http://www.haskell.org/~pairwise/intro/intro.html
3.---------------------------------------------------------------
En la programación declarativa es más fácil la verificación de los programas.
En programación imperativa no sólo importa los valores con los que se llaman, también depende el orden de la llamada al método, a los métodos del objeto y casi siempre, a cualquier cosa del programa. Esto provoca una explosión de posibilidades imposible de verificar.
4.---------------------------------------------------------------
Los lenguajes declarativos suelen tener un poder expresivo impresionante.
El caso más radical es Haskell. Probablemente el lenguaje más potente y expresivo.
Quizá para ser capaz de sacarle partido, es necesaria una capacidad especial.
5.---------------------------------------------------------------
Los lenguajes declarativos, especialmente Haskell tienen fama de no ser muy eficientes.
Creo que para ejemplos sencillos, que se pueden optimizar fácilmente en c/c++ (por ejemplo), Haskell puede estar detrás.
Pero para casos reales, grandes y complejos de optimizar, Haskell tiene ventajas importantes.
La evaluación perezosa, la optimización dinámica y que el compilador pueda elegir el orden de ejecución para buscar el más óptimo... seguramente produzcan un código muy eficiente, sin mucha preocupación al programador.
Sin estas herramientas, todos sabemos, que las optimizaciones son la principal fuente de errores en los programas.
6.---------------------------------------------------------------
Los lenguajes declarativos son naturalmente paralelizables
Aquí la diferencia es radical e incomparable.
Un ejemplo muy bueno está en el lenguaje Erlang.
Erlang es un lenguaje declarativo muy, muy sencillo (uno de los más sencillos que he visto en mi vida)
Está orientado a sistemas de ejecución paralela, distribuida, tolerante a fallos, ejecución continua...
Para el SO, crear un proceso es caro, conmutar un proceso es caro.
Es más barato con hebras (para eso se crearon), pero aún así sigue siendo un recurso caro (unos pocos miles es demasiado).
En Erlang, crear un proceso es increíblemente barato, y lo mismo para las conmutaciones, y lo mismo para el paso de mensajes (nada de numeritos, mensajes complejos)
Ejemplo en yaws (yet another web server). Comparación con apache.
http://www.sics.se/~joe/apachevsyaws.html
Esta comparación es salvaje, pero también es comparar dos productos en el punto fuerte de uno de ellos.
En 4000 peticiones simultáneas, Apache casca, demasiados procesos.
Mientas que yaws (erlang) da mejor rendimiento incluso para 80.000 peticiones simultáneas.
7.---------------------------------------------------------------
El futuro es la programación paralela, dicen algunos.
La velocidad de los micros se ha parado, ahora buscan potencia haciéndolos multinúcleo.
Intel dice que prevee meter hasta 100 núcleos.
¿Están los programas preparados para aprovechar estas nuevas configuraciones?
NO
¿Están los lenguajes de programación preparados para ayudar en este nuevo escenario?
Los imperativos no.
Aquí tenéis un artículo fantástico
http://www.gotw.ca/publications/concurrency-ddj.htm
8.---------------------------------------------------------------
La programación declarativa es extrictamente académica??
Seguro que no está tan difundida como la imperativa, pero muchos defienden que no es puramente académica.
Se utilizar en las universidades, por profesores e investigadores, porque probablemente es la mejor opción.
Erlang está funcionando en máquinas muy caras con unas cifras espectaculares.
Ericson está explotando Erlang en máquinas con programas de más de 3 millones de líneas de código, con una tasa de fallo de 31 milisegundos al año
http://www.erlang.se/publications/BYTE2003.html
9.---------------------------------------------------------------
La programación declarativa es mejor para cosas pequeñas.
Erlang ha demostrado que puede funcionar muy bien en proyectos enormes.
Exprogramadores imperativos dicen que la gran ventaja de Haskell es para programas grandes o enormes
http://www.haskell.org/~pairwise/intro/intro.html
Scala recomienda utilizar todo lo posible la programación declarativa para poder eSCALAr al máximo.
10.-------------------------------------------------------------
Gran parte de las novedades de los lenguajes imperativos, o son características declarativas, o son cosas que aparecieron antes en estos lenguajes.
11.-------------------------------------------------------------
Líneas de código, tiempo de desarrollo...
Algunas pruebas dicen que Haskell gana
http://www.haskell.org/papers/NSWC/jfp.ps
12.-------------------------------------------------------------
Un inconveniente con los lenguajes muy expresivos, es que hace difícil la vida a los IDE y los compiladores.
Para un IDE es mucho más difícil funciones como autocompletar.
Para un compilador es más difícil informar con precisión del error.
Ver caso de C++ (seguro que también le sucederá a Scala). Creo que le pasa a Haskell
miércoles, febrero 06, 2008
Matemáticas y beisbol
origen... http://www.historiasdelaciencia.com/?p=317#more-317
¿Qué relación hay entre el béisbol y los números primos? Aunque en el béisbol, al igual que en otros deportes, son muy importantes las estadísticas, en este artículo nos referimos a una relación bastante más curiosa e inesperada con las matemáticas, en particular, con los números primos. Y sobre ello y otras anécdotas versará nuestra historia de hoy.
El 8 de abril de 1974, Hank Aaron bateó un home run (en castellano se puede decir también “jonrón”): el numero 715 de su carrera. La importancia de este home run era que, con él, Aaron rompía la marca histórica que Babe Ruth estableció en 1935 y que estaba precisamente en 714.
Resulta que Carl Pomerance, un matemático que trabajaba en la ciudad de Atlanta, donde Aaron había bateado su home run 715, notó que los factores primos de 714 y 715 satisfacían una propiedad interesante.
Si factorizamos ambos números obtenemos las siguientes descomposiciones:
714 = 2 × 3 × 7 × 17
715 = 5 × 11 × 13
Si nos fijamos en las sumas de ambas factorizaciones tenemos que:
2 + 3 + 7 + 17 = 5 + 11 + 13 = 29
A los números que satisfacen esta propiedad, es decir, a los pares consecutivos cuya descomposición en factores primos tienen la misma suma, Pomerance les llamó pares de Ruth–Aaron. Y claro está, en cosas como esta, los ordenadores son fantásticos. Pomerance descubrió que entre los números menores que 20.000 hay 26 pares de Ruth–Aaron. El mayor en este rango lo forman el 18.490 y y el 18.491.
Aunque los pares disminuían en cantidad cuando los números crecían, Pomerance conjeturó que había infinitos pares de Ruth–Aaron, pero no tenía idea de demostrar su corazonada. Su descubrimiento fue publicado en un paper de tono desenfadado en el Journal of Recreational Mathematics. Una semana después de la publicación recibió una llamada de Paul Erdös, a quien no conocía. El maestro de la teoría de números le dijo que había demostrado la conjetura y que quería ser invitado a Atlanta para mostrarla. Esto de decir “quería ser invitado” debe ser matizado y sólo se entiende si conocemos un poquito más a este excéntrico y genial matemático, así que os recuerdo unos pocos detalles que, a buen seguro, harán vuestras delicias.
Reunía todos los clichés del sabio distraído y del genio desorganizado. Comenzó su fama como niño prodigio en Hungría. A los cuatro años de edad le dijo a su madre: “si sustraes 250 de 100, obtienes -150″. A esa misma edad era capaz de multiplicar cifras de tres y cuatro dígitos sólo de cabeza.
A los 18 años causó sensación en los círculos matemáticos de Hungría al presentar una prueba sencilla del teorema de Euclides que dice que entre cualquier número entero y su doble existe, al menos, un número primo. Esta prueba ya existía y la había dado el ruso Pafnuti Lvóvitch Chebyshef, pero su prueba era demasiado extensa para figurar en los libros de texto. Erdös había proporcionado, sin embargo, una prueba sencilla y simple.
Un día llamó a la puerta de una zapatería. La empleada salió a abrir. Después de las mínimas frases de introducción la conversación fue la siguiente:
- Dígame un número de cuatro cifras.
- 2.532 - respondió la dependienta.
- Su cuadrado es 6.411.024. Lo siento, estoy perdiendo facultades y no puedo darle el cubo. ¿Cuántas pruebas del teorema de Pitágoras conoce?
- Una.
- Yo conozco 37.
Y continuó un rato haciéndole preguntas de matemáticas.
De adulto sólo pensaba en matemáticas y se dice que incluso pensaba en ellas aunque estuviera pensando en otra cosa. Escribió, sólo y en colaboración con otros, un total de 1.475 artículos académicos, muchos de ellos imprescindibles y todos muy valiosos. Hizo matemáticas en 25 países diferentes, completando teoremas en lugares remotos y a veces publicándolos en revistas poco conocidas. En su época, se decía que alguien no era un verdadero matemático si no le conocía.
Le fascinaban los problemas fáciles de plantear pero difíciles de resolver. Tenía tanta manía matemática que cuando entraba en una habitación su primera observación era: “Cuatro paredes dividido por dos ventanas”. Sus cartas solían empezar normalmente con un “Supongamos que x es …”.
Medía un metro setenta, pesaba 49 kilos y tenía el pelo blanco, así que podemos decir que su aspecto era cadavérico, demacrado o enfermizo. Si a esto añadimos que cuando iba andando por la calle iba gesticulando, siempre sumido en las matemáticas, no sé qué más se podrá decir de él.
Sólo poseía una maleta, la ropa que llevaba puesta y una radio de la época de las cavernas. Decía que la propiedad privada era una carga. A principios de los setenta llegó como profesor invitado por un año. Después de cobrar su primera paga, un mendigo le pidió el dinero que costaba una taza de té. Erdös tomó el sobre, separó una cierta cantidad para sus gastos frugales y le dio el resto al mendigo. En 1984 le dieron el Premio Wolf, el más lucrativo en matemáticas con 50.000 dólares de premio. Se quedó con 720 dólares y el resto lo donó para que se hiciera un campamento para chicos con problemas de conducta. A finales de la década de los 80 supo de un estudiante que quería estudiar matemáticas pero que no podía por problemas de dinero. Le dio 1.000 dólares prestados y que sólo se los devolviera cuando hubiera arreglado dichos problemas. Una década más tarde el estudiante quiso devolvérselos y se lo dijo a Graham, un amigo común: “¿Erdös querrá que le pague con intereses?”. Cuando Graham se lo preguntó a Erdös le contestó: “Dile que haga con los 1.000 dólares lo mismo que hice yo”.
No tenía ocupación laboral estable: daba clases aquí y allá y conferencias, y así iba tirando. Renunció absolutamente a todas las comodidades materiales, incluso tampoco tenía domicilio fijo: vivía en casas de amigos allí donde le tocaba enseñar o hacer de conferenciante. Poseía un lenguaje peculiar. Los niños eran “épsilon” (en matemáticas, épsilon es un número muy pequeño), dar clases “predicar”, el matrimonio “captura” y Dios era “FS” (fascista supremo); las mujeres eran “jefes”, los hombres “esclavos”, los casados “atrapados”, la música era “ruido” y el alcohol “veneno”. Cuando decía que alguien había muerto significaba que había dejado de hacer matemáticas. Rechazaba toda religión organizada. Un día fue a dar clase a una escuela católica y dijo que lo único que le molestaba era que hubiera tantos signos “más” (+) en las paredes. En otra ocasión le preguntaron: “¿Qué dirías a Jesucristo si te lo encontraras en la calle?” y respondió que le preguntaría si la hipótesis del continuo era verdad. Daba tres posibilidades en la contestación que debía darle este último:
a) Gödel y Cohen ya había dicho todo lo que hay que saber.
b) Sí existe respuesta, pero tu cerebro no está lo suficientemente desarrollado para entenderla.
c) El Padre, el Espíritu Santo y Yo hemos estado elucubrando sobre el particular desde mucho antes de la Creación, pero no hemos llegado a ninguna conclusión.
Y añadía que esta última respuesta sería la más amable.
Una mañana, en Nueva Jersey, se mencionó el nombre de un colega de California. En ese momento, Erdös recordó un resultado matemático que quiso compartir con él. Se levantó y fue a marcar el número. Su anfitrión le recordó que en California eran las 5 de la mañana. Erdös respondió: “Muy bien, eso significa que estará en casa”.
Escribió con otros 485 autores, por lo que se puede decir que colaboró con más gente que cualquier otro matemático en la historia. A esos 485 se dice que tienen número de Erdös 1. Si alguien ha trabajado con uno de esos 485 se dice que tiene el número de Erdös 2. Si alguien con alguno de estos últimos tendrá el número de Erdös 3 y así sucesivamente. Einstein tenía número de Erdös 2. Aun cuando estuvo bien entrado en los 70, hubo algunos años en los que publicó 50 artículos. Los buenos matemáticos escriben ese orden de publicaciones … en toda su vida.
En 1976 George Purdy y otros matemáticos estaban tomando café en el salón de la Universidad de Texas. En la pizarra que quedaba a sus espaldas había un problema de análisis funcional, un campo extraño para Erdös. Purdy sabía que dos matemáticos acababan de dar con una solución del mismo que habían condensado en 30 páginas. Erdös miró a la pizarra y dijo: “¿Qué es eso? ¿Es un problema?”. Purdy le dijo que sí. Entonces, se dirigió a la pizarra y se concentró en los enunciados, hizo unas cuantas preguntas sobre qué representaban algunos símbolos y luego, sin esfuerzo, escribió la solución en dos líneas. Los que estaban presentes se quedaron estupefactos, como si hubieran asistido a un truco de magia.
Os podría contar muchas cosas más de este fascinante personaje, pero me extendería demasiado. Hay un maravilloso libro titulado “El hombre que sólo amaba los números” que cito en fuentes y que ya os recomendé que trata de la vida y peripecias de este hombre, su pasión por las matemáticas y su lado más humano.
Pero volvamos con Pomerance y los pares de Ruth-Aaron. El encuentro derivó en una colaboración que se plasmó en 21 publicaciones. En 1995, Hank Aaron y Paul Erdös recibieron el doctorado honoris causa de la Universidad de Emory. Erdös, si bien llevaba toga y birrete, también llevaba sus sandalias. Se sentó en el podio con la cabeza entre las manos garabateando sus cuadernos de matemáticas mientras duraba la ceremonia.
Pomerance explicó todo sobre los pares de Ruth-Aaron al propio jugador Hank Aaron, quien escuchó pacientemente lo que cambió la vida del propio Pomerance. Finalmente les pidió a ambos (a Erdös y a Aaron) que le autografiaran una pelota de béisbol, lo cual hicieron con gusto; y así, Pomerance afirmó: “Hank Aaron tiene número de Erdös uno”.
Os dejo finalmente con una frase que a Erdös le gustaba decir:
Un matemático es una máquina que convierte café en teoremas.
Estos matemáticos están locos.
Fuentes:
“El hombre que sólo amaba los números“, Paul Hoffman.
Un buen resumen del libro anterior
lunes, febrero 04, 2008
operación de EQUIVALENCIA en Java y Scala JVM
Capítulo 21 ScalaBook, lectura imprescindible
Especialmente para programadores Java y .net, pero muy práctico para todos
Trata sobre "¿este objeto es igual que este otro?"
Dice que en Java, se ha verificado que lo raro es encontrar este método correctamente sobreescrito (muy raro)
Es muy raro encontrar un programador de Java que sobreescriba la relación de equivalencia correctamente
Y eso puede tener consecuencias muy malas
¿Qué opina Scala de todo esto?
Primero...
El libro insiste como nadie en como debe hacerse correctamente para que no te equivoques.
Eso ayuda, pero... no es una ayuda impresionante.
Por ejemplo, Groovy (lenguaje compilado pero dinámico para la máquina virtual de Java) siempre te crea un operador de igualdad y función Hash correctas, tú puedes sobreescribirlo si quieres, pero, por defecto tienes algo que funciona
Si en Scala creas "case class" en vez de class normal, Scala te creará una función Hash y operador de comparación correctos
¿Porqué sólo si es una "case class"?
Quizá por rendimiento, pero lo importante es que si no es una "case class" funciona igual de mal que Java.
Tienes una función Hash y una función de equivalencia, que sólo sirven para dar problemas
¿No sería mejor en estos casos no tener nada y que explotara en tiempo de compilación?
Sí, pero en Java, son métodos definidos en Object. Por lo tanto todos tienen que tener implementación.
Como Java NUNCA da una implementación de estos automática para tus clases, y como es muy frecuente que tus clases no necesiten estos métodos... Java opta por...
No te voy a dar el coñazo obligándote a definir unos métodos que casi nunca te sirven para nada. Yo en Object ya te doy una implementación.
Majete que es el colega... no te da por saco continuamente, pero... eso provoca uno de los mayores puntos de error en Java (porque el pobrecito no tiene ni idea en Object de como se comparan manzanas)
Error que sólo se detecta en tiempo de ejecución y puede ser difícil de encontrar
La conclusión es que Scala en este punto es mucho mejor que Java, pero sigue sin ser una solución buena (véase Groovy)
Como siempre (y en este caso también), la recomendación de Scala es... no utilices clases con estado (asignación destructiva). Eso ayuda
¿Y QUÉ PASA CON LAS TUPLAS?
Las tuplas son inmutables (no tienen estado, no tienen asignación destructiva). Empezamos bien
Aunque en el libro no recuerdo haber leído nada al respecto, he podido comprobar que Scala sí crea método de equivalencia y Hash correctamente.
Muy buena noticia
En C++ no tienen esta paranoia
pos eso, ya me diréis como lo veis
He vuelto a leer sobre paralelismo, concurrencia, tolerancia a fallos... y me paso al lado tenebroso...
Programación declarativa, esa es la solución a los problemas de hoy y sobre todo del futuro (a no ser que llegue antes la computación cuántica de forma masiva y todos al paro)
Si me dejáis (es decir, si no recibo cientos de correos pidiendo que no os torture con eso), os iré contando
Por cierto...
¿Alguien se atreve a intentar explicarme cómo se comparan dos objetos en visual basic 6?
Es curiosidad porque no tengo ni idea
Suscribirse a:
Entradas (Atom)